Таблица 2
|
Номера звеньев/ название |
Схема |
Класс/ подвижность |
Вид контакта/ замыкание |
|
0-1/ поступательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
|
1-2/ поступательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
|
2-3/ сферическая |
|
5/1 |
поверхность (низшая)/ геометрическое |
|
3-4/ поступательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
|
4-5/ вращательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
 |
Данный пространственный рычажный механизм представляет собой одну простую, незамкнутую кинематическую цепь. К стойке присоединено одно подвижное звено. Для определения подвижности механизма, воспользуемся формулой Сомова- Малышева:
![]()
![]()
 Чтобы определить маневренность механизма,
воспользуемся следующей формулой:
Чтобы определить маневренность механизма,
воспользуемся следующей формулой:
![]()
![]()
Степень подвижности механизма и его маневренность равны, следовательно, результаты структурного анализа пространственного механизма верны.
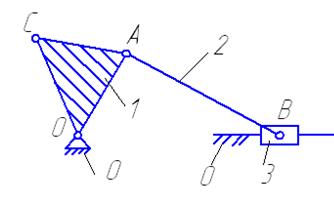
Рис. 2
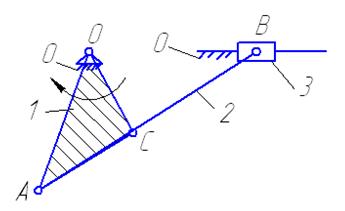
 Задание 2. Структура плоского рычажного механизма
представлена на рис. 2. Пронумеруем по порядку арабскими цифрами подвижные звенья
, а буквами латинского алфавита- все подвижные соединения. Структурная схема
рассматриваемого механизма содержит 3 звена: звено 1- кривошип, представляющий
собой составное звено, образованное неподвижным соединением трех простых
звеньев, совершает вращательное движение и имеет три вершины; звено 2- шатун,
совершает сложное движение и имеет две вершины; звено 3- ползун, движется
поступательно и имеет одну вершину.
Задание 2. Структура плоского рычажного механизма
представлена на рис. 2. Пронумеруем по порядку арабскими цифрами подвижные звенья
, а буквами латинского алфавита- все подвижные соединения. Структурная схема
рассматриваемого механизма содержит 3 звена: звено 1- кривошип, представляющий
собой составное звено, образованное неподвижным соединением трех простых
звеньев, совершает вращательное движение и имеет три вершины; звено 2- шатун,
совершает сложное движение и имеет две вершины; звено 3- ползун, движется
поступательно и имеет одну вершину.
Выявленные кинематические пары и их параметры представлены в табл. 3.
Таблица 3
|
Кинематич. пара/ название |
Схема |
Класс/ подвижность |
Вид контакта/ замыкание |
|
0-1/ вращательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
|
1-2/ вращательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
|
2-3/ вращательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
|
3-0/ поступательная |
|
5/1 |
поверхность (низшая)/ геометрическое |
 Данный механизм представляет собой одну простую,
замкнутую цепь. К стойке присоединено два элемента: кривошип 1 и ползун 3. Этот
плоский рычажный механизм не содержит дефектов.
Данный механизм представляет собой одну простую,
замкнутую цепь. К стойке присоединено два элемента: кривошип 1 и ползун 3. Этот
плоский рычажный механизм не содержит дефектов.
Для определения степени подвижности, воспользуемся формулой
Чебышева:
![]()
![]()
 Для
решения второй задачи структурного анализа разобьем рассматриваемый механизм на
структурные группы Ассура:
Для
решения второй задачи структурного анализа разобьем рассматриваемый механизм на
структурные группы Ассура:
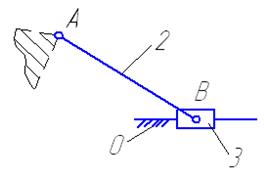
I структурная группа Ассура состоит из группы звеньев 3-2 (рис. 3), в которую входят:
два подвижных звена- шатун 2 и ползун 3;
два поводка- кривошип 1 и направляющая 0;
три кинематические пары:
1-2 вращательная пара 5 класса;
2-3 вращательная пара 5 класса;
рис.3 3-0 поступательная пара 5 класса; тогда
![]()
![]()
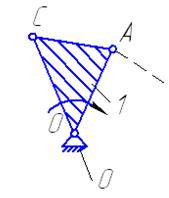
Вторя группа звеньев 0-1 (рис.4) состоит из одного подвижного звена- кривошипа 1, и стойки 0, и, одной кинематической пары:
0-1 вращательная пара 5 класса; тогда
![]()
![]()
Следовательно группа звеньев 0-1 представляет собой первичный механизм с подвижностью W=1.
Структурная формула механизма:
![]()
![]()
![]()
![]()
Таким образом, данный плоский рычажный механизм обладает одной степенью свободы. А так как группа звеньев 3-2 является структурной группой Ассура 2 класса 2 порядка 2 вида, то и данный механизм 2 класса.
рис.4
Задание 3. Для выпо лнения метрического синтеза найдем масштабный
коэффициент по формуле:
лнения метрического синтеза найдем масштабный
коэффициент по формуле:
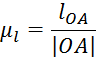
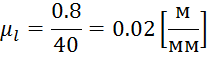
Остальные размеры звеньев вычислим по формуле:
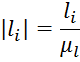
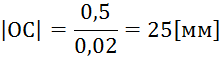
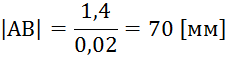
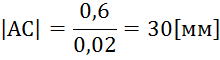
Построим положения звеньев механизма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.