группирования элементов в ступени профилактики растет совокупная стоимость РТВ, а затраты на устранение внезапных (аварийных) отказов уменьшаются. Это происходит из-за более точного учета оптимального технического ресурса элементов автомобиля, так как при большем количестве ступеней профилактики Z происходит более дифференцированное группирование элементов. Поэтому существует точка [СППРmin; Zopt], при которой минимизируется целевая функция. Целевую функцию оптимизации системы профилактики АТС запишем в следующем виде:
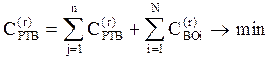 (3.1)
(3.1)
где: ![]() -
эксплуатационные затраты системы профилактики АТС в год, руб.;
-
эксплуатационные затраты системы профилактики АТС в год, руб.;
![]() -
эксплуатационные затраты на проведение прогнозируемых разновидностей
профилактики АТС в год, руб.;
-
эксплуатационные затраты на проведение прогнозируемых разновидностей
профилактики АТС в год, руб.;
![]() - эксплуатационные затраты на устранение
не прогнозируемых (аварийных) отказов АТС в год, руб.;
- эксплуатационные затраты на устранение
не прогнозируемых (аварийных) отказов АТС в год, руб.;
n - количество РТВ; N . количество АТС в выборке.
Рассмотрим технологию группирования элементов автомобиля в РТВ. Для определения первой составляющей целевой функции необходимо знать периодичности, номенклатуру и наименование (шифры) элементов, входящих в РТВ, а также перечень элементарных технологических операций. Для оценки второй составляющей используем параметры надежности, полученные в реальных условиях эксплуатации. В результате аппроксимации целевой функции получены оптимальные интервальные значения разновидностей периодических профилактик.
На последующих этапах рассматривается модель формирования ступени профилактики с учетом стратегий процесса восстановления. Формирование элементов в ступени профилактики осуществляется по следующему алгоритму. Из множества N деталей, узлов и агрегатов АТС с множеством значений их периодичности L0, по классификационным признакам, разделим на детали, лимитирующие безопасность дорожного движения и экологию окружающей среды с периодичностью L1, в первом случае. Во – втором, на детали, лимитирующие надежность с точки зрения экономической целесообразности их дальнейшего использования по назначению L2. Затем множество значений оптимальной периодичности L0={L0i | i = 1,2,.,N} разделим на два подмножества. При этом оба подмножества должны отвечать следующему условию: L1ÎL0, L2ÎL0 и L1ÇL2= Æ. Причем на практике L1<<L2 (см. рис.2.4).Для определения периодичности множеств L1, L2 введем шифры элементов, которые имеют флаг 0 - для массива L2; 1 - для массива L1.В общем случае периодичность множества L0 имеют разные значения и являются величинами стохастическими с размахом в пределах множества равным
L= L max - L min, тыс. км.
Разделим его на Z промежутков длиной
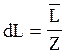 , тыс. Км (3.2)
, тыс. Км (3.2)
[L min + dL×(k-1), L min + dL -k), k=1,2,...,Z (3.3)
и
[L max - dL, Lmax] (3.4)
В соответствии с полученными полуинтервалами (3.3) и промежутком (3.4) группируем периодичность замены множества L0 на Z групп. В итоге получим семейство подмножеств {L0j | j = 1, 2,., Z} множества L0, которое в свою очередь делится на два семейства {L1j|j = 1,2,.,Z} и {L2j|j = 1,2,.,Z}. Таким образом, получены интервалы попадания случайных событий – отказов.
В пределах каждого интервала группирования, образуются свои центры - периодичности группирования случайных событий, которые определим по следующему алгоритму. Пусть L3 - есть центр значений периодичности, образующий группу, включающую множество элементов с примерно равной наработкой. Если L1j ¹ Æ и N1j - количество элементов множества L1j.
L3j = min {L1ji Î L1j}, i=1,2,..,N1j. (3.5)
Ограничение (3.5) объясняется требованиями безопасности дорожного движения, охраны окружающей среды и стремлением снизить затраты на устранение отказов.
В случае если L1j = Æи L2j ¹ Æ и если N2j - количество элементов множества L2j, то, применив метод наименьших квадратов, получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.