Анализ научно-исследовательских работ по работоспособности, надежности транспортных средств (на примере топливного насоса ВАЗ 2108)

2. Модель оценивания показателей долговечности ТС

2.1 Оценка среднего технического ресурса до первой замены Топливного насоса ВАЗ 2108 (точечная оценка)

Вариационный ряд:

220  86  152 92  108  268  252  208  198  184  172  111  233  248  192  177 161  152 148 132 122

Количество членов вариационного ряда N=21

Выборочная средняя наработка, тыс. км:

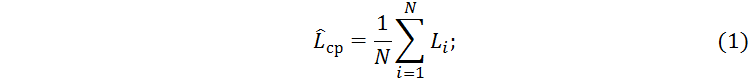
Подставив значения, получим

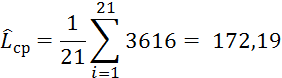
Дисперсия точечной оценки средней наработки до отказа, (тыс. км)²:

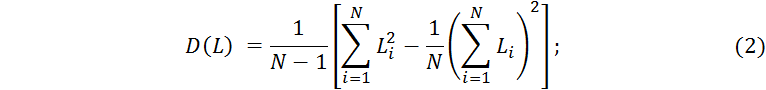
Подставив значения, получим

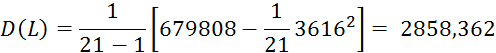
Среднее квадратическое отклонение, тыс. км:

 

Получим

Коэффициент вариации точечной оценки средней наработки до отказа

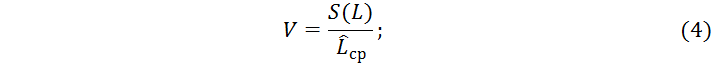
Подставив полученные значения, получаем

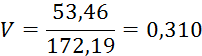
По табл. 1  в соответствии с полученным значением определяем параметр формы b закона Вейбулла- Гнеденко:                                      

2.2 Расчет доверительного интервала среднего технического ресурса ТС

С вероятностью  можно утверждать, что средняя наработка до замены рассматриваемого элемента АТС находится в интервале , что и является интервальной оценкой.

Нижняя и верхняя границы данного интервала следующие:

Расчетное значение предельной относительной ошибки

                              

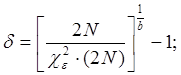
Определим  при, для чего рассчитаем уровень значимости ε и выберем по таблице 2  значение

Уровень значимости задают в зависимости от требуемой точности оценки средней наработки до отказа

Следовательно, получим

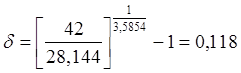
Границы доверительного интервала, тыс. км:

   

Действительное значение средней наработки до отказа находится в интервале [151,87 тыс. км, 192,51 тыс. км] с вероятностью 0,90.      

2.3 Оценка параметра масштаба закона Вейбулла – Гнеденко

Точечная оценка параметра масштаба закона Вейбулла - Гнеденко, тыс. км:

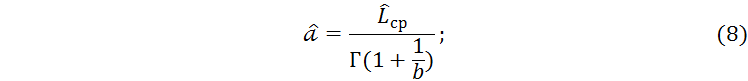
где  – гамма-функция, выбранная из таб. 4 в зависимости от коэффициента вариации V. Получим  0,9009   

Подставив полученные значения, получаем

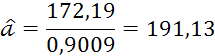
Граничные значения интервальной оценки, тыс. км:

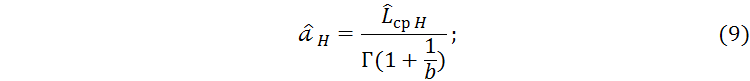
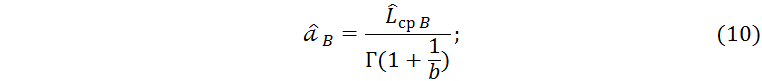
Получаем

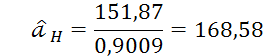
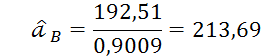
Прежде чем перейти к оценке остальных показателей надежности, необходимо проверить принятую в п.1 нулевую гипотезу о соответствии экспериментального распределения отказов распределению Вейбулла-Гнеденко.

2.4 Проверка нулевой гипотезы

Соответствие закона Вейбулла-Гнеденко экспериментальному распределению проверяем по - распределения согласия Пирсона. Нет оснований для отклонения нулевой гипотезы при соблюдении условия:

где

 значение критерия, вычисленное по экспериментальным данным;

 критическая точка (табличное значение) критерия при уровне значимости  и числе степени свободы k.(Берем из табл. 2).

Уровень значимости принимаем β = 0,05

Число степеней свободы

     где

S – количество частичных интервалов выборки;

r – количество параметров предполагаемого распределения.

При двухпараметрическом законе Вейбулла-Гнеденко .

Нулевая гипотеза проверяется по следующему алгоритму:

2.4.1 Количество интервалов S по правилу Штюргеса с округлением до целого значения

Количество интервалов

Получим

Число степеней свободы

Исходя из того что k = 3, принимаем  ²_табл=6,3.

Найдем отношение размаха вариационного ряда на число интервалов т.е. разность между наибольшим и наименьшим значениями вариационного ряда:

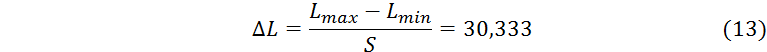
Получим

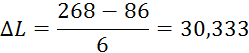
Определим границы интервалов

Получим

Таблица 1. – Расчет эмпирических частот

2.4.2 Теоретические частоты

Функция распределения отказов

                              

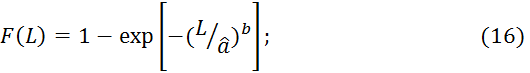
где

L - средняя наработка на отказ (тыс.км);

а - точная оценка параметра закона Вейбулла – Гнеденко в тыс. км.

Получим

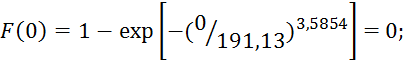
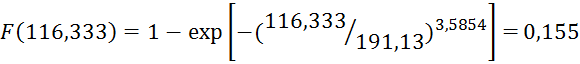
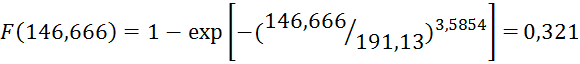
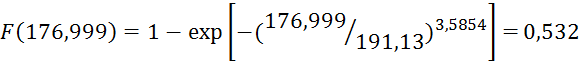
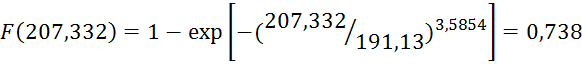
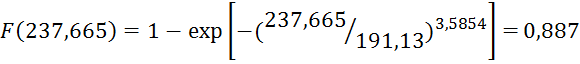
Рассчитаем ∆F(Lj), результаты занесем в таблицу 2.

∆F(L₁) = 0,155 - 0 = 0,155

∆F(L₂) =0,321 - 0,155 = 0,166

∆F(L₃) =0,532 - 0,321 = 0,211

∆F(L₄) =0,738 - 0,532 = 0,206

∆F(L₅) = 0,887 – 0,738 = 0,149

∆F(L₆) = 1- 0,887 = 0,113

Найдем _j, результаты занесем в таблицу 2.

Таблица 2 – Расчет 𝜒²-критерия согласия Пирсона

j	Lj-1	Lj+1	nj	nj2	∆F(Lj)	j
1	0	116,333	4	16	0,155	3,255	4,915
2	116,333	146,666	2	4	0,166	3,486	1,147
3	146,666	176,999	5	25	0,211	4,431	5,642
4	176,999	207,332	4	16	0,206	4,326	3,698
5	207,332	237,665	3	9	0,149	3,129	2,876
6	237,665	∞	3	9	0,113	2,373	3,793
итого:		∑ nj = 21		∑ΔF(Lj)=1,000		∑j =21	∑ = 22,071

2.4.3 Определение расчетного значения критерия

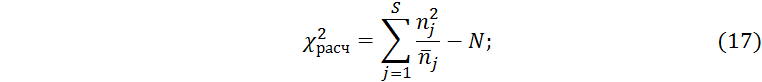
Получим

 

Из таблицы 2, при  и , принимаем

В результате получим 

   условия выполнены.

Нулевая гипотеза о распределении Вейбулла-Гнеденко принимается.

3. Оценка количественных характеристик безотказности и долговечности.

3.1 Оценка вероятности безотказной работы

Известно, что вероятность безотказной работы и вероятность отказа составляют вероятностную группу событий:

Вероятность безотказной работы

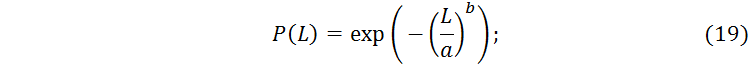
Подставив значения при, получим

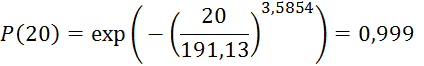
По данной формуле рассчитаем  для других значений пробега, результат занесем в таблицу 3.

Определим интервальную оценку , подставив граничные значения

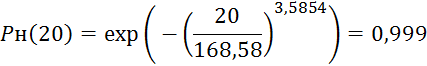
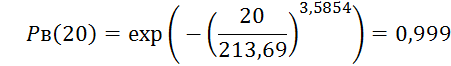
Рассчитаем  для других значений пробега, результат занесем в таблицу 3.

Таблица 3- Расчетные данные вероятности безотказной работы (нижняя и верхняя доверительные границы) топливного насоса до первой замены автомобиля ВАЗ 2108

L	P(L)	Pн(L)	Pв(L)
0	1	1	1
20	0,999	0,999	0,999
40	0,996	0,991	0,996
60	0,984	0,969	0,985
80	0,956	0,920	0,963
100	0,906	0,840	0,924
120	0,828	0,725	0,865
140	0,720	0,584	0,784
160	0,589	0,431	0,684
180	0,446	0,287	0,569
200	0,308	0,169	0,448
220	0,190	0,087	0,331
240	0,104	0,030	0,228
260	0,049	0,014	0,145
280	0,019	0,004	0,084
300	0,006	0,001	0,044
320	0,001	0,0001	0,020
340	0,000	0,000	0,008
360	0,000	0,000	0,003
380	0,000	0,000	0,001
400	0,000	0,000	0,0002

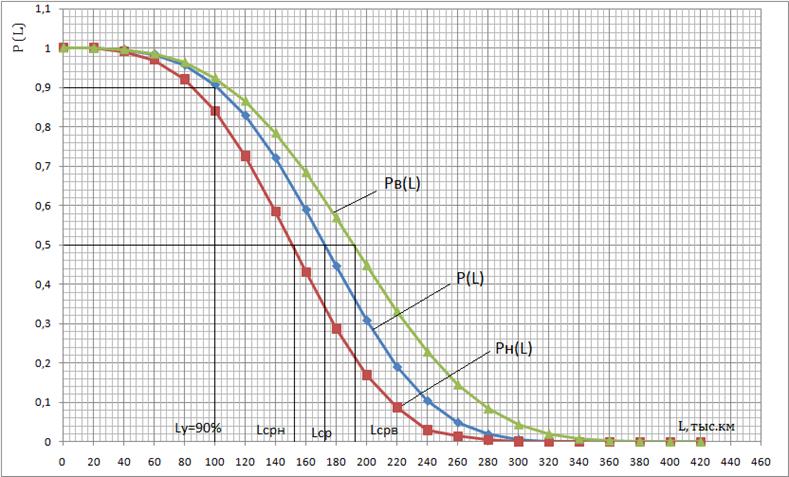
Рисунок 1 – График вероятности безотказной работы до первой замены топливного насоса, автомобиля ВАЗ 2108.

3.2 Оценка гамма – процентной наработки до отказа

Гамма – процентной наработки до отказа , тыс.км, – это наработка, в течении которой отказ элемента АТС не возникает с вероятностью .

Для закона Вейбулла – Гнеденко его точечная оценка:

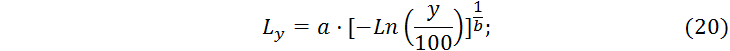
при

Для нормального закона  может быть рассчитана аналитически из формулы