Машиностроение \ Автомобили

Дифференциалы автомобилей: Краткое методическое пособие (Кинематика, динамика и основы расчета шестерен дифференциала), страница 8

Число зубьев

Угол зацепления , профиль эвольвентный, высота зуба нормальная

Угол зацепления , высота зуба нормальная

Угол зацепления , с укороченной высотой зуба

10

0,056

0,064

0,083

11

0,061

0,072

0,092

12

0,067

0,078

0,099

13

0,071

0,083

0,103

14

0,075

0,088

0,108

15

0,078

0,092

0,111

16

0,081

0,094

0,115

17

0,084

0,096

0,117

18

0,085

0,098

0,120

19

0,088

0,100

0,123

20

0,090

0,102

0,125

21

0,092

0,104

0,127

23

0,094

0,106

0,130

25

0,097

0,108

0,133

27

0,099

0,111

0,136

30

0,101

0,114

0,139

34

0,104

0,118

0,142

38

0,106

0,122

0,145

43

0,108

0,126

0,147

50

0,110

0,130

0,151

60

0,113

0,134

0,154

75

0,115

0,138

0,158

100

0,117

0,142

0,161

250

0,119

0,146

0,165

300

0,122

0,150

0,170

Рейка

0,124

0,154

0,175

Напряжение изгиба у основания зуба полуосевой шестерни (25), МПа

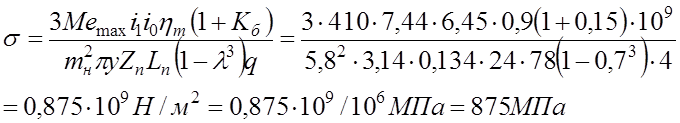
Допускаемое напряжение  . Превышение составляет 60%, то есть в 1,6 раза.

Подобное превышение допустимо по следующим причинам /5/:

а) вышеприведённая методика является приближённой и даёт немного завышенные величины напряжений;

б) превышение напряжений имеет место лишь на первой передаче, время работы на которой грузового автомобиля составляет всего (0,5-1,0)%. На второй передаче  напряжения будут составлять:

;

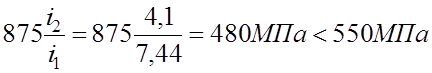в) небольшие скорости полуосевых шестерён и сателлитов при движении на первой передаче, что обеспечивает режим их работы, близкий к статическому.

Для расчёта удельных давлений на различные поверхности сателлитов (27), (28), (29) необходимо начертить эскиз сателлита в масштабе 1:1 (рисунок 7).

Зная торцовый (окружной модуль) , рассчитываем диаметр наружной окружности сателлита по большому конусу

 

Полученный диаметр является основанием ас (см. рисунок 7) равнобедренного треугольника оас, стороны которого являются образующими сателлита.

Половина диаметра  вместе с конусным расстоянием , образуют прямоугольный треугольник, высоту которого ое можно определить по теореме Пифагора

 .

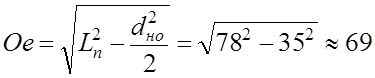
Зная Ое, можно, взяв за основание , построить треугольник с вершиной в точке «О» и сторонами . Это и есть «каркас» сателлита.

Нормальный модуль был подсчитан ранее , а высота        зуба .

Размер (диаметр) шипа крестовины  принят по прототипу. Остальные размеры показаны на эскизе (см. рисунок 6).

Длина зуба, мм

.

Удельное давление на опорную поверхность оси сателлита в шестерне (27), МПа

.

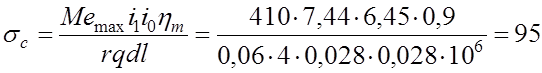Удельное давление на ось сателлита в месте закрепления её в коробке дифференциала, МПа

.

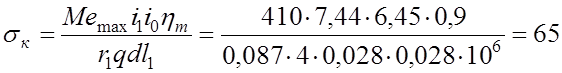Удельное давление по торцу сателлита, МПа

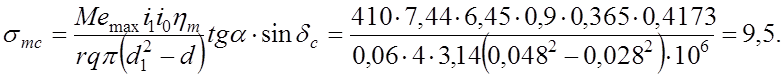
Допускаемое удельное давление 70 МПа. Лишь в первом случае  МПа незначительно превышает допустимое.


Библиографический список

1 Андреев, Б. В. Теория автомобиля: Учебное пособие/ Б. В. Андреев. Красноярск: КГУ,1984.

2 Гольд, Б. В. Теория, конструирование и расчёт автомобиля: Учебник/Б. В. Гольд, Б. С. Фалькевич. М.: Машгиз, 1957.

3 Гольд, Б. В. Конструирование и расчёт автомобиля: Учебник/ Б. В. Гольд. М.: Машгиз, 1962.

4 Гришкевич, А. И. Проектирование трансмиссий автомобилей: Учебник/ А. И. Гришкевич и др. М.: Машиостроение, 1984.

5 Курганов, А. И. Основы расчёта шасси тракторов и автомобилей: Учебник/ А. И. Курганов. М.: Государственное издательство сельскохозяйственной литературы, 1953.

6 Кригер, А. М. Шасси автомобиля ЗИЛ-130/ под ред. А. М. Кригер. М.: Машиносроение, 1973.


Содержание

1 Назначение, классификация дифференциалов. Преимущества и недостатки. 2

2 Принцип действия и кинематика шестерёнчатого симметрического дифференциала. 3

3 Принцип действия дифференциала с механизмом свободного хода (МСХ) 6

4 Влияние типа межколёсного дифференциала на проходимость автомобиля (динамика дифференциала) 7

5 Методика расчёта шестерёнчатого симметричного дифференциала. 14

6 Пример расчёта шестерёнчатого симметричного дифференциала. 17

Библиографический список. 23

Скачать файл