Экономико-математические приемы анализа. Эвристические (психологические) приемы анализа

3. 4. Экономико-математические приемы анализа

 В реальных условиях хозяйствования на предприятие оказывают влияние множество факторов (рис.2). Часто невозможно определить прямую связь между изменением результативного показателя и всеми факторами, как это представлено в детерминированном анализе. Многие из них  оказывают косвенное  воздействие на протекающие экономические процессы, поэтому целесообразно использовать приемы стохастического (вероятностного) анализа.

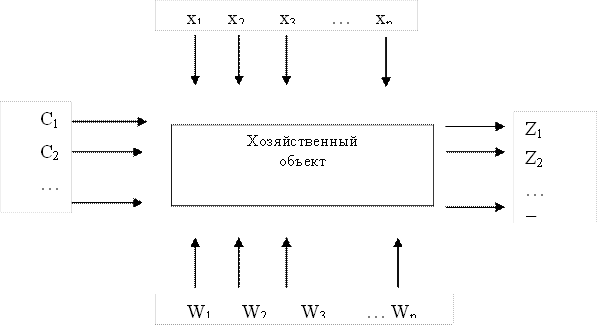
Рис. 2. Модель хозяйственной системы

C_1, …, Сn – входные факторы (параметры системы), не изменяющиеся в процессе принятия управленческого решения. Например, производственные площади, оборудование, количество рабочих дней в году.

х_1, …, х_n – регулируемые факторы, например, величина ресурсов, увеличение сменности работы и др.

z_1, …, z_n – количественные и качественные характеристики результатов функционирования системы. Например, себестоимость, объем продукции и услуг. Это есть переменные величины, т.е. функции от показателей С и Х.

W_1, …, W_n – неконтролируемые (случайные) факторы. Их появление и количественная оценка заранее неизвестны: аварии, стихийные бедствия, разрыв хозяйственных связей и др.

Дисперсионный анализ используется для оценки влияния факторов, зависящих от деятельности анализируемого предприятия: анализ прибыли, рентабельности, производительности труда, использования основных производственных фондов, анализ использования новой техники, технологии и т.д.

Посредством этого метода анализируются результаты наблюдений, зависящих от различных, одновременно действующих факторов и дается оценка величины их влияния. Результаты могут изменяться за счет влияния набора случайных факторов, имеющих случайные величины. Задача дисперсионного анализа – оценить соотношение между факторами для определения существенности или несущественности различий условий наблюдения.

На практике дисперсию часто используют для объективного отражения вариации какого-либо множества факторов по формуле средних квадратов отклонений показателей:

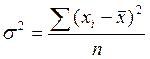
Корреляционный анализ – наиболее распространенный прием стохастического моделирования хозяйственного процесса, если взаимосвязь между показателями не является строго функциональной и искажена влиянием посторонних, случайных факторов. Основное назначение корреляции – нахождение и оценка взаимосвязи исследуемого показателя и факторов, определяющих их уровень.

Корреляционная связь может быть прямой, если с ростом (снижением) значений факторных показателей происходит рост (снижение) результативного показателя, и обратной, если рост факторного показателя вызывает снижение результативного и наоборот. Различают две формы связи: прямолинейная(уравнение прямой линии) и криволинейная (уравнение параболы, гиперболы и др.).

Для измерения связи между двумя переменными используется формула определения коэффициента парной корреляции:

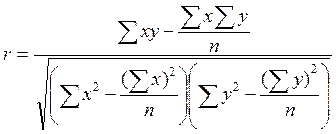 , где х – значение  факторного показателя; у - значение результативного показателя; n- число данных в выборке.

Величина коэффициента парной корреляции находится в пределах от. Положительное значение r характеризует прямую связь между результативным признаком и факторным, отрицательное значение показывает обратную связь. Близость значения r к свидетельствует о тесноте связи между признаками. При связь отсутствует, если же , то связь между показателями является детерминированной.

В практических расчетах могут встречаться ситуации, когда переменные могут быть измерены не достаточно достоверно или точно. В этом случае целесообразно использовать формулу коэффициента