Составление программы вычисления корней биквадратного уравнения. Построение графика заданной функции

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Сибирский федеральный университет»

Институт космических и информационных технологий

Кафедра «Информационные системы и технологии в металлургии»

КОНТОРОЛЬНАЯ РАБОТА

Дисциплина: «Имитационное моделирование технологических систем в ЦМ»

Преподаватель                                  ______________                        Л.А. Лапина

подпись, дата                                           инициалы, фамилия

Студент      ЗИС - 061999                 ______________                       А.В. Баженов

код (номер) группы                              подпись, дата                                           инициалы, фамилия

Красноярск 2011 г.

1. Составить программу вычисления корней биквадратного уравнения   х²-5х +4 = 0. Получит М-файл в виде function.

Создадим в MATLAB Blank M-File

Листинг:

function [x1, x2] = qvad (a, b, c)

d = b^2 - 4*a*c;

x1 = (-b + sqrt (d))/2*a;

x2 = (-b - sqrt (d))/2*a;

Решение:

>> [x1, x2] = kvad (1, -5, 4)

x1 =

4

x2 =

1

2. Построить графики функций:

а);

Решение:

x= -10:0.01:10;

y=((1+x).*(x.^2+2.*x-2)).^1/3;

plot(x,y);

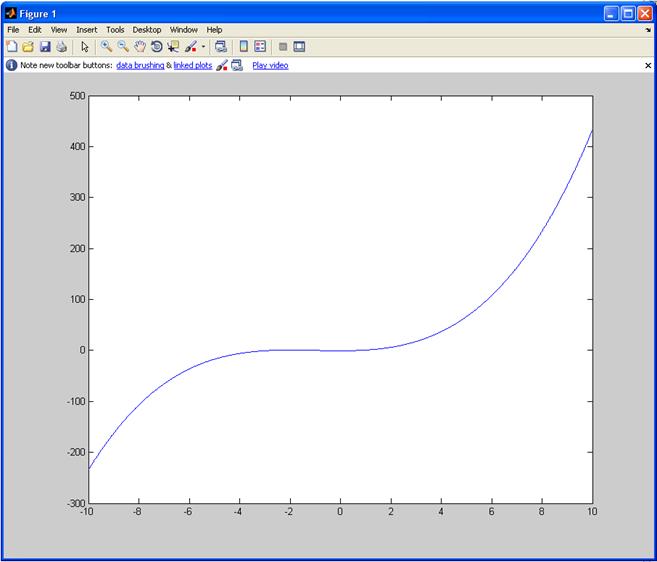
б) ;

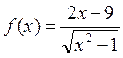Решение:

Заданная функция существует на всей оси, кроме интервала [-1, 1], т.е. на концах интервала функция стремится к бесконечности. Поэтому, нужно задать аргументы для левой [-10; -1) и правой (1; 10] частей графика.

x= -10:0.01:-1.01;

y=(2.*x-9)./((x.^2-1).^(1/2));

plot(x,y);

hold on

t=1.01:0.01:10;

z=(2.*t-9)./((t.^2-1).^(1/2));

plot(t,z);

grid on

title('График разрывной функции');

xlabel('X');

ylabel('Y');

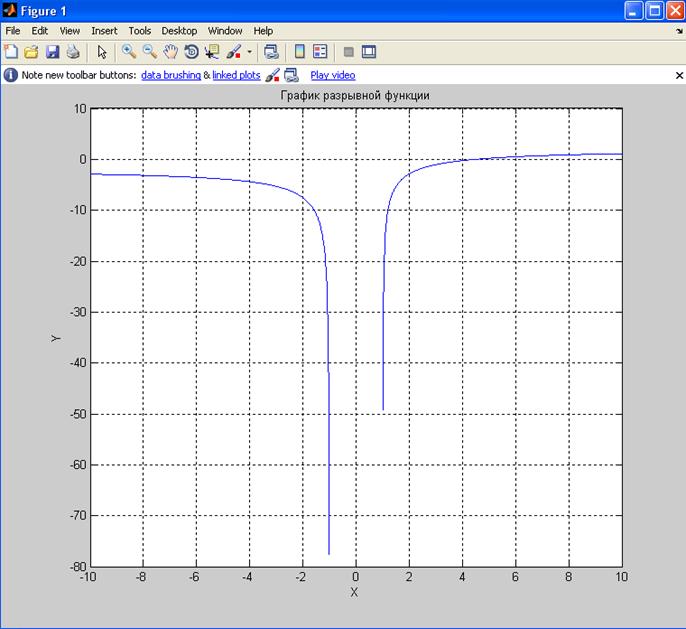
в) ;

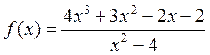Решение:

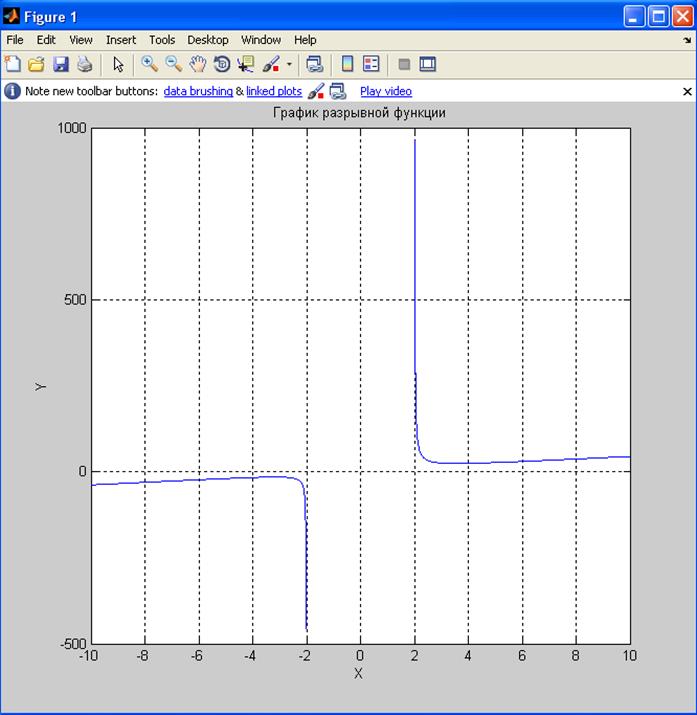
Заданная функция существует на всей оси, кроме интервала [-2, 2], т.е. на концах интервала функция стремится к бесконечности. Поэтому, нужно задать аргументы для левой [-10; -2) и правой (2; 10] частей графика.

x= -10:0.01:-2.01;

y=(4.*x.^3+3.*x.^2-2.*x-2)./(x.^2-4);

plot(x,y);

hold on

t=2.01:0.01:10;

z=(4.*t.^3+3.*t.^2-2.*t-2)./(t.^2-4);

plot(t,z);

grid on

title('График разрывной функции');

xlabel('X');

ylabel('Y');

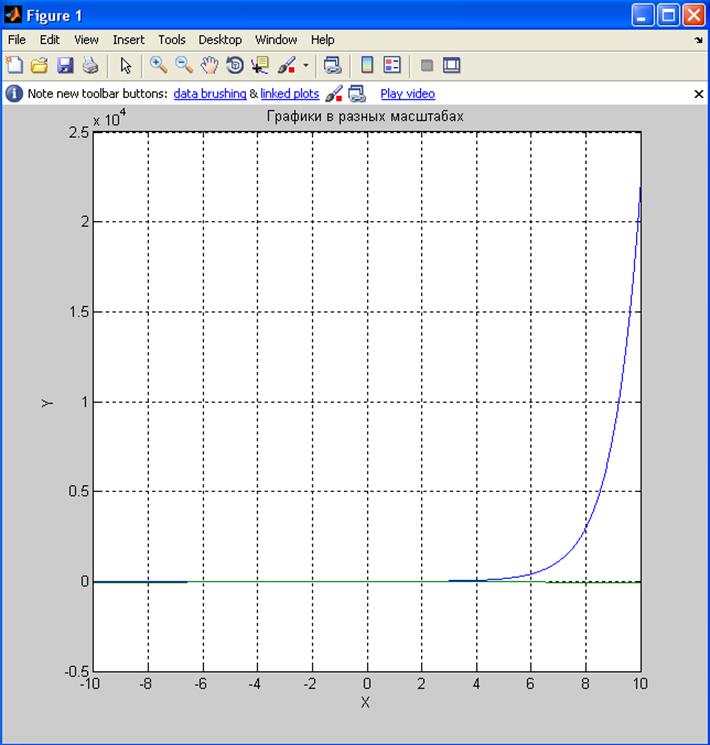
3.  Построить графики двух функций в одной области:

Решение:

x=-10:0.01:10;

y=exp(x);

z=2-x.^2;

plot(x,y,x,z);

grid on

title('Графики в разных масштабах');

xlabel('X');

ylabel('Y');

4. Построить на плоскости кривую, заданную в параметрическом виде:

a) ;

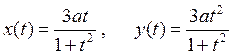Решение:

a=10;

t=-10:0.01:10;

x=(3.*a.*t)./(1+t.^2);

y=(3.*a.*t.^2)./(1+t.^2);

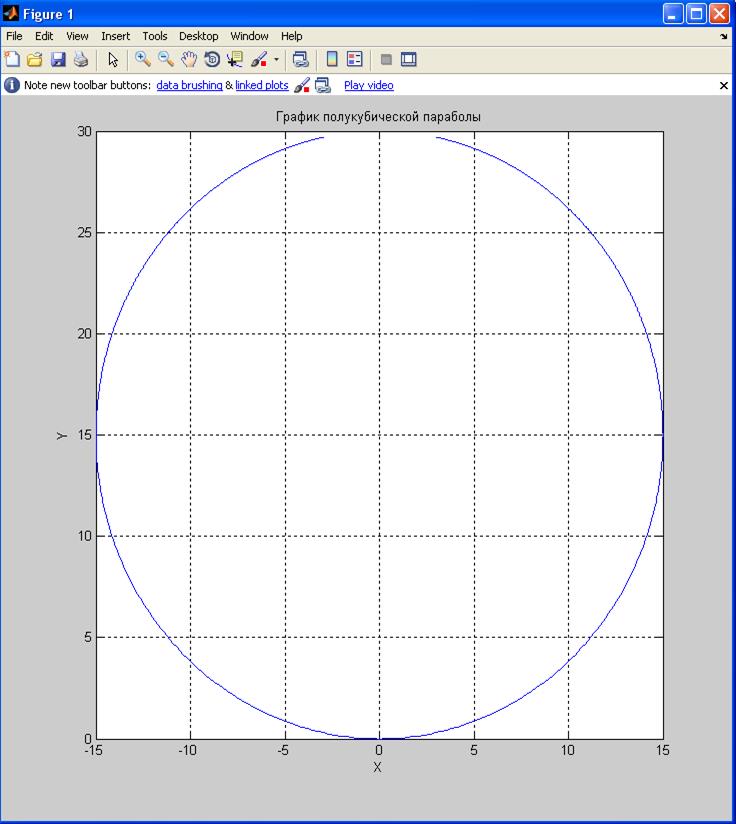
plot(x,y);

grid on;

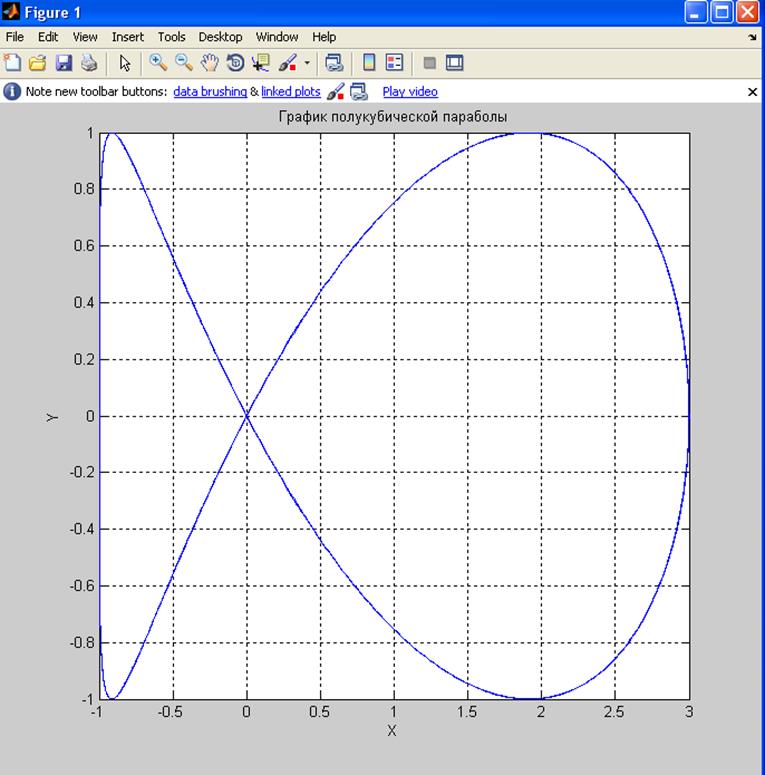
title('График полукубической параболы');

xlabel('X');

ylabel('Y');

          б)

Решение:

a=10;

t=-10:0.01:10;

x=cos(t).^2+2.*cos(t);

y=2.*sin(t).*cos(t);

plot(x,y);

grid on;

title('График полукубической параболы');

xlabel('X');

ylabel('Y');

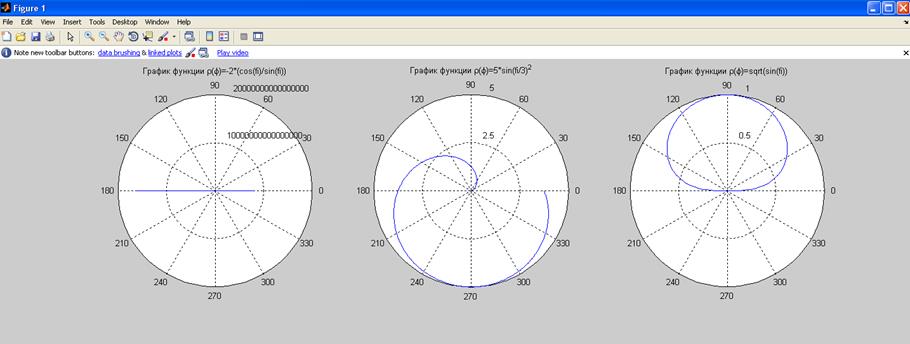
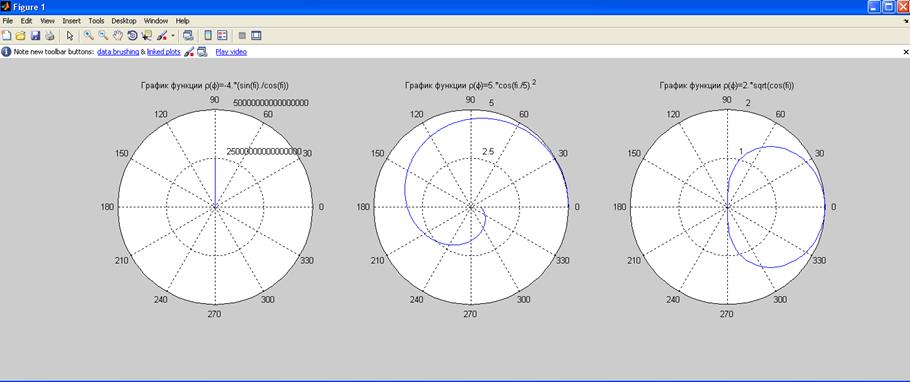
5. Изобразить кривые, заданные в полярных координатах:

          а)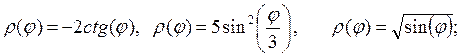

Решение:

fi=0:pi/200:2*pi;

ro=-2.*(cos(fi)./sin(fi));

ro1=5.*sin(fi./3).^2;

ro2=sqrt(sin(fi));

subplot(1,3,1);

polar(fi,ro);

title('График функции \rho(\phi)=-2*(cos(fi)/sin(fi))');

subplot(1,3,2);

polar(fi,ro1);

title('График функции \rho(\phi)=5*sin(fi/3)^2');

subplot(1,3,3);

polar(fi,ro2);

title('График функции \rho(\phi)=sqrt(sin(fi))');

б)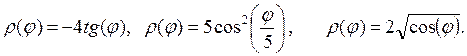

Решение:

fi=0:pi/200:2*pi;

ro=-4.*(sin(fi)./cos(fi));

ro1=5.*cos(fi./5).^2;

ro2=2.*sqrt(cos(fi));

subplot(1,3,1);

polar(fi,ro);

title('График функции \rho(\phi)=-4.*(sin(fi)./cos(fi))');

subplot(1,3,2);

polar(fi,ro1);

title('График функции \rho(\phi)=5.*cos(fi./5).^2');

subplot(1,3,3);

polar(fi,ro2);

title('График функции \rho(\phi)=2.*sqrt(cos(fi))');

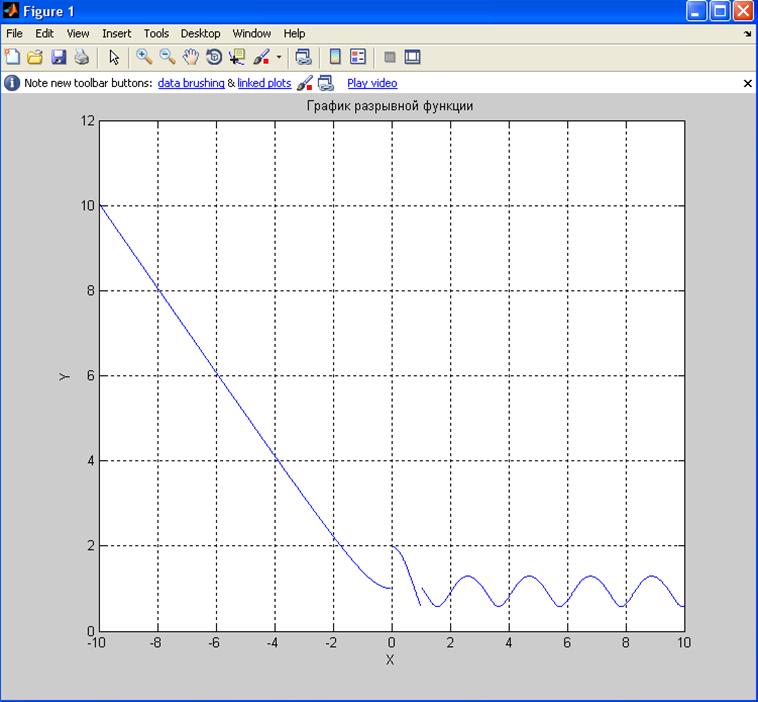
6. Построить график заданной функции

         

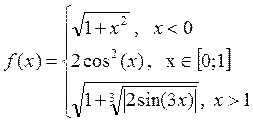
Решение:

x=-10:0.01:-0.01;

y=sqrt(1+x.^2);

plot(x,y);

hold on

t=0:0.01:1;

z=2.*cos(t).^2;

plot(t,z);

grid on

k=1.01:0.01:10;

m=sqrt(1+(2.*sin(3.*k)).^1/3);

plot(k,m);

grid on

title('График разрывной функции');

xlabel('X');

ylabel('Y');

7. Выполнить построение поверхностей различного типа:

a)z(x,y) = x² – 2y²;

[x y]=meshgrid(-4:4,-5:5)

x =

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4