Информатика и выч. техника \ Имитационное моделирование

Составление программы вычисления корней биквадратного уравнения. Построение графика заданной функции, страница 2

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

-4    -3    -2    -1     0     1     2     3     4

y =

-5    -5    -5    -5    -5    -5    -5    -5    -5

-4    -4    -4    -4    -4    -4    -4    -4    -4

-3    -3    -3    -3    -3    -3    -3    -3    -3

-2    -2    -2    -2    -2    -2    -2    -2    -2

-1    -1    -1    -1    -1    -1    -1    -1    -1

0     0     0     0     0     0     0     0     0

1     1     1     1     1     1     1     1     1

2     2     2     2     2     2     2     2     2

3     3     3     3     3     3     3     3     3

4     4     4     4     4     4     4     4     4

5     5     5     5     5     5     5     5     5

z=x.^2-2.*y.^2

z =

-34   -41   -46   -49   -50   -49   -46   -41   -34

-16   -23   -28   -31   -32   -31   -28   -23   -16

-2     -9     -14   -17   -18   -17   -14    -9    -2

8      1      -4     -7     -8     -7     -4      1      8

14    7      2      -1     -2     -1      2      7     14

16    9      4       1      0      1      4       9     16

14    7      2      -1     -2     -1      2      7     14

8     1     -4      -7     -8     -7     -4      1      8

-2    -9    -14    -17   -18   -17   -14    -9    -2

-16   -23   -28   -31   -32   -31   -28   -23   -16

-34   -41   -46   -49   -50   -49   -46   -41   -34

mesh(x,y,z);

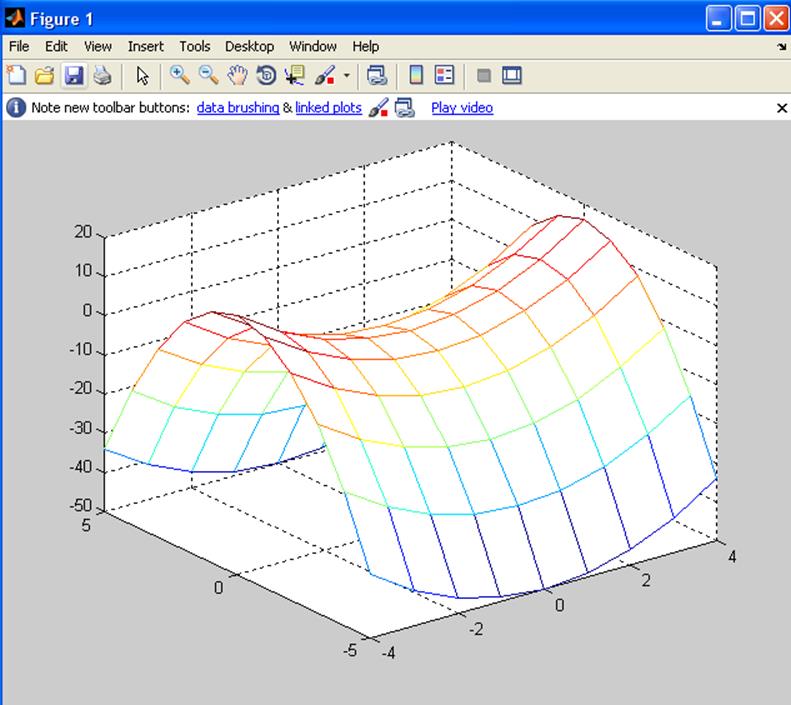
b)z(x,y)=3x2 – 2 sin2(y) y2;

[x y]=meshgrid(-4:0.1:4,-4:0.1:4);

z=(3.*x.^2)-(2.*sin(y).^2.*y.^2);

surf(x,y,z);

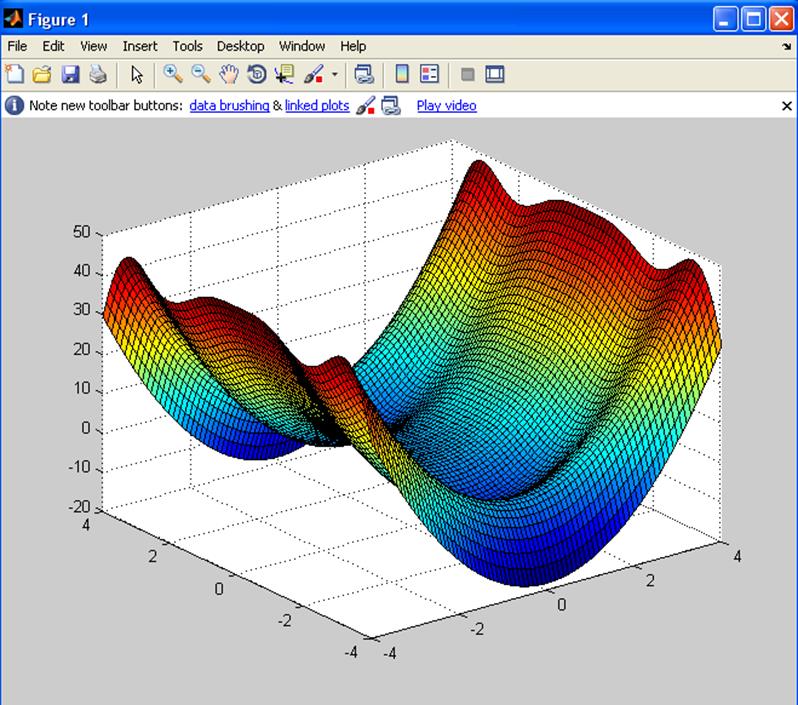
c)z(x,y)=3e2x x – 2 y;

[x y]=meshgrid(-4:0.1:4,-5:0.1:5);

z=(3.*exp(2.*x).*x)-(2.*y);

mesh(x,y,z);

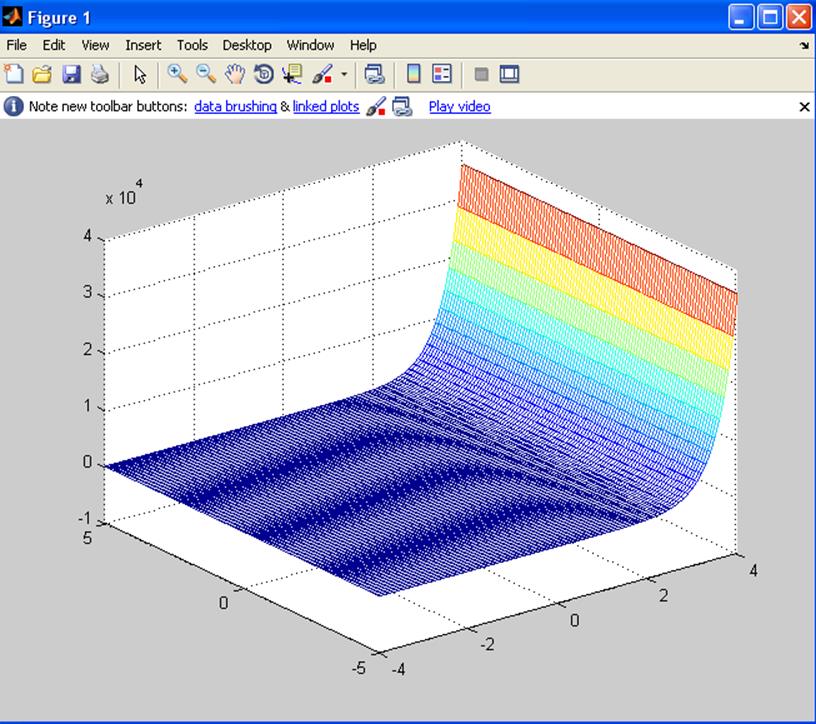
d)

[x y]=meshgrid(-4:0.1:4,-5:0.1:5);

z=(sin(x)./y).*cos(y./x);

mesh(x,y,z);

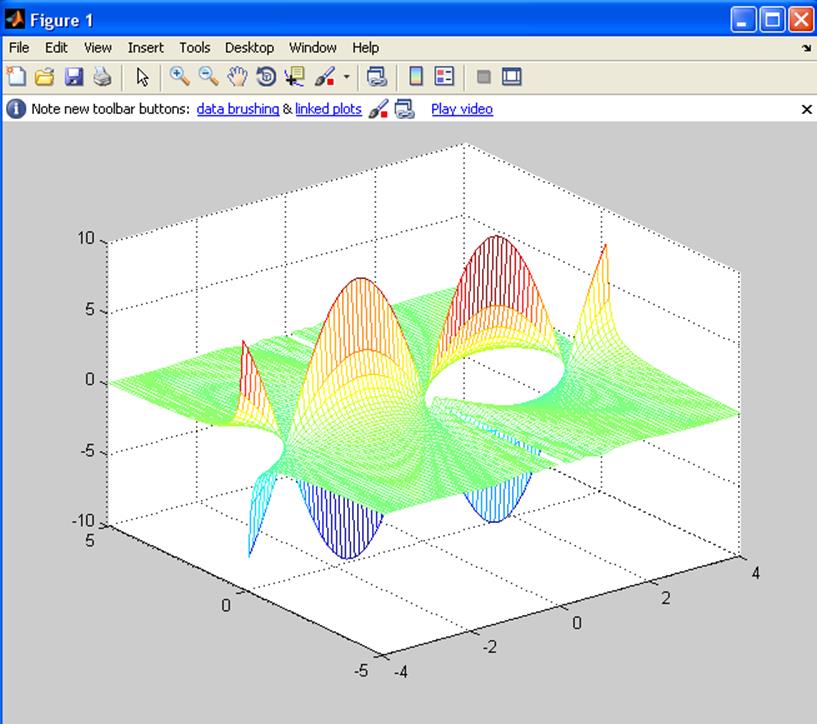
e)

>> [x y]=meshgrid(2:0.1:4,0:0.1:2);

z=log(x.^2-y.^2);

mesh(x,y,z);

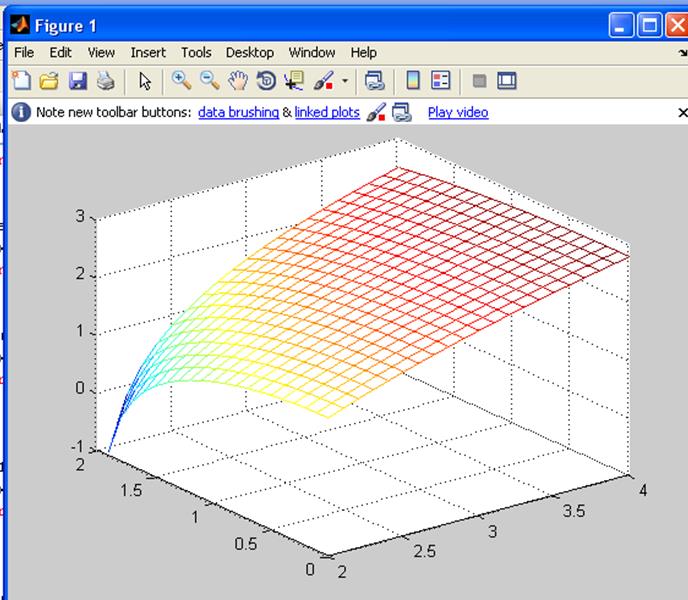
f)

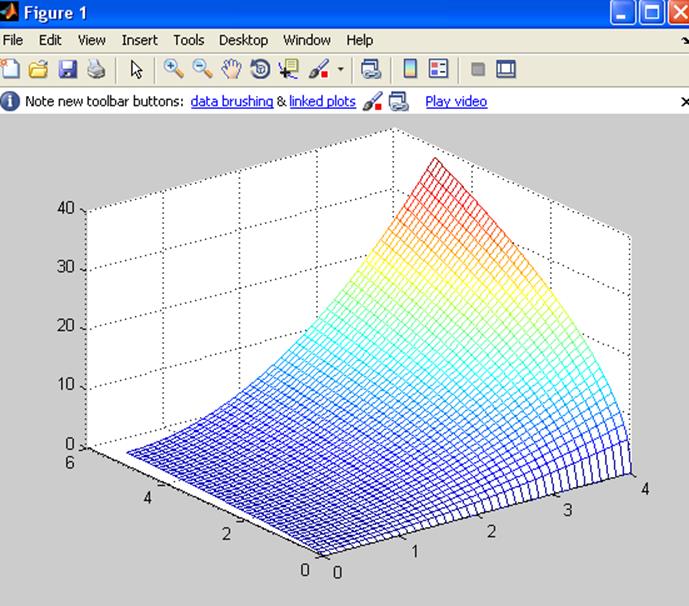
[x y]=meshgrid(0:0.1:4,0:0.1:5);

z=sqrt(y).*(x.^2+1);

mesh(x,y,z);

8.Дано устройство, состоит из трёх узлов. Чтобы это устройство функционировало, все три узла должны работать. Узел I выходит из строя лишь при неисправности обоих элементов A и B, вероятности безотказной работы которых в течение заданного интервала времени, равны P(A) = 0,8; P(B) = 0,7. Узел II неисправен, если элемент C выходит из строя. Вероятность безотказной работы элемента C в течение заданного интервала времени составляет P(C) = 0,95. Узел III выходит из строя, когда одновременно неисправны все его элементы D, E и F. Вероятности безотказной работы элементов D, E и F в течение заданного интервала времени P(D) = 0,85, P(E) = 0,9, P(F)= 0,7.

Требуется определить вероятность безотказной работы устройства с помощью имитационного моделирования простых событий.

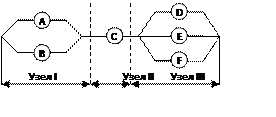
Схема устройства

9.Построить модель, с помощью которой можно делать прогнозы о ходе случайного процесса и подбирать значения параметров, обеспечивающих его устойчивость. Время, определяющее течение процесса, считать дискретным, поэтому все величины, характеризующие состояние процесса, маркируйте  моментами времени t = 1, 2, ….

          Требуется смоделировать следующий случайный процесс. На начала моделирования (t=0) в цехе имеется n однотипных исправных станков. Любой исправный станок к следующему моменту может выйти из строя с вероятностью p, т.е. стать неисправным. Имеется u рабочих, каждый из которых может заниматься ремонтом одного неисправного станка. В любой момент времени в ремонте может находиться определенное количество  станков и любой из них к следующему моменту может быть отремонтирован с вероятностью q, т.е. стать исправным.

          Исходные данные: всего в цехе станков n = 100;

          количество исправных станков на начало моделирования m = 100; 

число рабочих в цехе u = 10;

вероятность выхода из строя станка    p = 0,05;

вероятность выхода станка из ремонта   q = 0,2;

период моделирования Т=100 ( t = 0, 1, 2, …, 99).

На основе результатов моделирования выполнить следующее:

1.  Сделать прогноз о количестве исправных станков в каждый момент времени и на конец периода моделирования.

2.  Определить оптимальное число рабочих  в цехе, занимающихся ремонтом станков,  которые бы обеспечивали устойчивое состояние исправных станков.

Скачать файл