Разработка программы имитационного моделирования событий простых событий (Лабораторная работа № 4)

Лабораторная работа № 4 «Имитационное моделирование простых событий»

Тема: Программирование в MATLAB. Разработка программы имитационного моделирования событий простых событий.

Цель: Освоение операторов программирования. Выполнить задание 1.

Все М-файлы (с расширением .m) можно разделить на два класса: М-программы и М-функции. М-программа состоит из операторов на встроенном в MATLAB языке программирования (часто называют М-языком) и обращений к встроенным функциям MATLAB.

Создание М-программ. Основные операторы М-языка

Каждая такая программа хранится в файле с расширением .m (создается в редакторе), для ее выполнения достаточно в командном окне (Command Window) ввести имя файла (без расширения), в котором хранится программа.

Оператор присваивания

Структура:    a=b, где a – имя переменной, b– значение или выражение.

Пример 1

% Определяем матрицу М размером 3×2

M=[1 3 5;6.7 9 9.12]

% Определяем переменную q– как строку символов

q=’Пример строки’

% Определяем переменную b, вычислив ее значение по формуле

b=sin(2/7)+cos(3/11)

% Дополняем переменную b, как матрицу 5×5, определив ее значение b(5,5)

b(5,5)=13

Организация простейшего ввода-вывода в диалоговом режиме

Для вывода результатов на экран можно просто не ставить «;».

Для ввода исходных данных в диалоговом режиме – функция input.

a=input(‘подсказка’);

Для вывода можно использовать функцию disp.

disp(b)

b – имя переменной или заключенный в кавычки текст.

Условный оператор

ifусловие

операторы1

else

            операторы2

end

Если условие истинно, то выполняются операторы1, если ложно – операторы2.

В качестве логических значений используются 1 («истина») и 0 («ложь»).

Операции отношения

Выполняют сравнение двух операндов и определяют, истинно выражение или ложно. Определены следующие операции отношения: < (меньше), > (больше), == (равно), ~= (не равно), <= (меньше или равно), >= (больше или равно).

Логические выражения

Выполняются над логическими данными. В табл. 1 представлены основные  логические выражения: «и», «или», «не».

Таблица 1. Логические операции

А	В	«не» А	А «и» В	А «или» В
0	0	1	0	0
0	1	1	0	1
1	0	0	0	1
1	1	0	1	1

Существует возможность представления логических выражений в виде логических операндов и операций (табл.2).

Таблица 2. Виды логических выражений

Тип выражения	Выражение	Логический оператор	Логическая операция
Логическое «и»	A and  B	and(A, B)	A & B
Логическое «или»	A or B	or(A, B)	A | B
Отрицание	not A	not (A, B)	~ A

В логических выражениях используются логические операции, операции отношения, например (a+x)>(c+d*cos(y))|(a>b). Логические операторы (выражения) определены и над массивами (матрицами) одинаковой размерности и выполняются над каждым из элементов. В итоге формируется результирующий массив (матрица) логических значений, каждый элемент которого вычисляется путем выполнения логической операции над соответствующими элементами исходных массивов.  При одновременном использовании в выражении логических и арифметических операций возникает проблема последовательности их выполнения.  Принят следующий приоритет операций:

1. Логические операторы.
2. Логическая операция ~.
3. Транспонирование матриц, операции возведения в степень, унарный + и -.
4. Умножение, деление.
5. Сложение, вычитание.
6. Операции отношения.
7. Логическая операция «и» - &.
8. Логическая операция «или» - |.

Пример 2

>> a=3; b=4; c=6.123;

>> m=~(((a+b)*c)>a^b)|(a+b)==((b-a)+a^2)

m =

            1

>>d=~or((b-a)>b, (b-a)>a)

d =

            1

>>x=[1 2 4; 5 6 1; 2 7 9]

x =

            1   2   4

            5   6   1

            2   7   9

>>y=[3 1 6; 2 8 0; 4 2 11]

y = 

            3   1   6

            2   8   0

            4   2   11е

>>g= ~or((x>2*y), (x>y))| and((x>2*y),(x<y))

g =

            1   0   1

            0   1   0

            1   0   1

Пример 3

Написать на М-языке программу нахождения действительных корней квадратного уравнения ax² + bx +c = 0.

a=input(‘a=’);

b=input(‘b=’);

c=input(‘c=’);

% Вычисление дискриминанта

d=b^2-4*a*c

% если дискриминант отрицателен, то

ifd<0

% вывод сообщения об отсутствии действительных корней

disp(‘Дискриминант отрицателен!!! Корней нет’)

% иначе

else

% вывод сообщения, что уравнение имеет два корня.

disp(‘Уравнение имеет два корня’)

% вычисление этих корней

x1=(-b+sqrt(d))/2/a

x2=(-b-sqrt(d)/2/a

end

Запуск программы из командной строки

>>primer3

a=1

b=2

c=-1

d =

8

Уравнение имеет два корня

x1 =

            0.4142

x2 =

            -2.4142

Расширенная форма оператора if

if   условие 1

                        операторы 1

elseif  условие 2      

операторы 2

elseif  условие 3

                        операторы 3

            …

elseif  условие n

                        операторы n

else

                        операторы

end

Пример 4

Написать на М-языке программу нахождения действительных корней биквадратного уравнения ax⁴ +bx² + c = 0.

Алгоритм

1. Ввод коэффициентов уравнения a, b, c.
2. Вычисление дискриминант уравнение d.
3. Если d≥ 0, определяются у₁ и у₂, а иначе корней нет.
4. Если у₁, у₂  < 0, то корней нет.
5. Если у₁, у₂  ≥ 0, то вычисляются четыре корня по формулам  ,  и выводятся значения корней.
6. Если условия 4 и 5 не выполняется, то необходимо проверить знак у₁. Если у₁  ≥ 0, то вычисляется два корня по формуле . Если  у₂  ≥ 0, то два корня рассчитываются по формуле . Вычисленные значения корней выводятся.

a=input(‘a=’);

b=input(‘b=’);

c=input(‘c=’);

d=b^2-4*a*c;

ifd<0

disp(‘Действительных корней нет’);

else

            y1=(-b+sqrt(d)/2/a;

            y2=(-b-sqrt(d)/2/a;

if (y1<0) & (y2<0)

                        disp(‘Действительных корней нет’);

elseif (y1>=0) & (y2>=0)

disp(‘Четыре действительных корня’);

x1=sqrt(y1)

x2=-x1

x3=sqrt(y2)

x4=-x3

else

disp(‘Два действительных корня’)

if y1>=0

                        x1=sqrt(y1)

                        x2=-x1

else

                        x1=sqrt(y2)

                        x2=-x1

                        end

end

end

            Оператор альтернативного выбора

switchпараметр

caseзначение 1

                        операторы 1

caseзначение 2

                        операторы 2

caseзначение 3

                        операторы 3

            …

otherwise

                        операторы

end

Операторы цикла

Оператор while

whileусловие

                        операторы

end

Оператор for

forx=xn:hx:xk

                        операторы

end

Если шаг цикла hx=1, то

forx=xn:xk

                        операторы

end

Оператор breakпрерывает выполнение цикла.

Оператор continueпрерывает выполнение текущего шага цикла.

Ввод-вывод массивов и матриц

Пример 5

N=input(‘N=’);

for i=1:N

            x(i)=input(strcat(‘x(‘,int2str(i),’)=’));

end

Пример 6

N=input(‘N=’);

M=input(‘M=’);

for i=1:N

        for j=1:M

            a(i,j)=input(strcat(‘a(‘,int2str(i),’,’,int2str(j),’)=’));

       end

end

Для вывода приглашений вида x(i)= и a(i,j)=  функции input использовались функции для работы со строками: strcat(s1, s2, …, sn) и int2str(d). Функция strcat– объединяет строки s1, s2, …, snв одну строку. Функцияint2str преобразует число dв строку символов.

Встроенные функции:

sum– нахождение суммы элементов массива;

prod– произведение элементов массива;

max, min– максимальный, минимальный элемент массива ,(матрицы);

sort– сортировка элементов массива.

ВЫПОЛНИТЬ ЗАДАНИЕ 1. ПРЕДСТАВИТЬ ПРОГРАММУ МОДЕЛИРОВАНИЯ

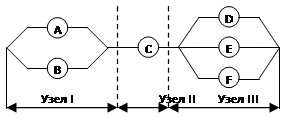Задание 1.  Дано устройство, состоит из трёх узлов (рис. 5.1). Чтобы это устройство функционировало, все три узла должны работать. Узел I выходит из строя лишь при неисправности обоих элементов A и B, вероятности безотказной работы которых в течение заданного интервала времени, равны P(A) = 0,8; P(B) = 0,7. Узел II неисправен, если элемент C выходит из строя. Вероятность безотказной работы элемента C в течение заданного интервала времени составляет P(C) = 0,95. Узел III выходит из строя, когда одновременно неисправны все его элементы D, E и F. Вероятности безотказной работы элементов D, E и F в течение заданного интервала времени