ЛАБОРАТОРНАЯ РАБОТА № 3
Тема: Форматирование графиков. Трехмерные графики. Анимация
Цель: Освоение средств форматирования графиков, создания трехмерных графиков и анимации.
Форматирование двумерных графиков
В MATLAB графики можно модифицировать, используя возможности графического окна.
ПРИМЕР 1. Построить точечный график функции у(х), заданной таблично (табл. 1) и график функции S(t) = -0,77t3 + 1,99t2 – 93,729 на интервале [10; 20].
Таблица 1. Табличная зависимость у(х)
|
х |
10,1 |
10,2 |
10,3 |
10,8 |
10,9 |
11 |
11,1 |
11,4 |
12,2 |
13,3 |
13,8 |
14 |
14,4 |
14,5 |
15 |
15,6 |
15,8 |
17 |
18,1 |
19 |
|
у |
24 |
36 |
26 |
45 |
34 |
37 |
55 |
51 |
75 |
84 |
74 |
91 |
85 |
87 |
94 |
92 |
96 |
97 |
98 |
99 |
Сформировать массивы x, y, S и t и построить график функции у(х) с помощью функции plot.
x=[10.1 10.2 10.3 10.8 10.9 11 11.1 11.4 12.2 13.3 13.8 14 14.4 14.5 15 15.6 15.8 17 18.1 19];
y=[24 36 26 45 34 37 55 51 75 84 74 91 85 87 94 92 96 97 98 99];
t=10:0.1:20;
S=-0.77*t.^3+1.99*t.^2-93.729;
plot(x,y);
В результате, вместо точечного графика получилась ломанная линия. Можно изменить обращение к функции plot, но рассмотрим модификацию графика с помощью средств графического окна. Для начала форматирования любого элемента графического окна необходимо выделить с помощью кнопки выбора, после чего двойным щелчком мыши перейти к форматированию выделенного объекта. Выделить ломанную и после перехода в режим форматирования линии в нижней части окна появится окно редактора свойств (PropertyEditor) выделенной линии. Изменить следующие параметры:
· DisplayName– имя графика, по этому имени можно будет обратиться к графику из программы и модифицировать его свойства с помощью функции set(позже);
· PlotType– тип изображенного графика, кроме обычных графиков (тип Line) есть возможность изображать и различные диаграммы;
· XDataSource– определяет массив Х точек графика;
· У DataSource– определяет массив У точек графика;
· ZDataSource– определяет массив Z точек для трехмерного графика;
· Поля, расположенные правее Line, позволяют изменить тип линии, ее толщину и цвет;
· Поля, расположенные правее Marker, позволяет изменить тип маркера, его размер и цвет.
Для изображения точечного графика установите тип линии – NoLine, тип маркера · размером 20.
Изменить любой объект на графике можно и с помощью контекстного меню.
Добавить график функции S(t) в графическом окне. Для этого выделить оси и в контекстном меню выбрать команду AddData… В появившемся меню установить следующие параметры добавляемого графика:
· Plot type – plot;
· XDataSource – t;
· У DataSource – S.
Изобразить линии сетки – выделить оси и в контекстном меню включить флажок Grid.
Включить легенду – в этом же контекстном меню включить флажок ShowLegend(на графике появится легенда).
Установить наилучшее расположение легенды – дважды щелкнув по легенде, вызвать окно редактора свойств (PropertyEditor) легенды и установить в нем LocationBest(наилучшее месторасположение). Можно было оставить и LocationManual(установка месторасположения вручную) и передвинуть легенду в нужное место с помощью мыши. Сам текст легенды частично отражает данные графика, для изменения текста выделить его и ввести новый.
Добавьте заголовок графика – Insert®Title и ввести текст График функций y(x) и S(t).
Добавьте подписи к осям Х и У – Insert®XLabel и Insert®YLabel, после чего введите подписи x, tи у, S.
Многие из рассмотренныхвозможностей форматирования графика доступны не только из контекстного меню, но и из главного окна графика.
Среди особенностей работы с графиком в графическом окне есть возможность сохранения графика в виде графического файла – File®Saveas в большинстве распространенных графических форматов.
В MATLAB 7 появилась возможность генерации кода М – программы, выполнение которой приведет к построению форматированного графика – File®GenerateM – file…
Трехмерные графики
Для построения графика поверхности z = f(x, y) необходимо выполнить следующие действия:
1. Сформировать в области построения графика прямоугольную сетку, проводя прямые, параллельные осям y =yiи x =xi, где xi = x0 + ih, h=(xn– x0) / n, i = 0, 1, 2, …,n, yj = y0 + jD, D=(yk– y0) / k, j = 0, 1, 2, …,k.
2. Вычислить значения zij = f(xi, yi) во всех узлах сетки.
3. Обратиться к функции построения поверхности, передавая ей в качестве параметров сетку и матрицу Z = (zij) значений в узлах сетки.
Для формирования прямоугольной сетки использовать функцию meshgrid.
ПРИМЕР 2. Построить график функции z(x, y) = y2 – x2, где х Î [-2; 2], y Î [-3; 3].
>>[x y]=meshgrid(-2:2,-3:3)
x =
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
y=
-3 -3 -3 -3 -3
-2 -2 -2 -2 -2
-1 -1 -1 -1 -1
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
>> z=y.^2-x.^2
z=
5 8 9 8 5
0 3 4 3 0
-3 0 1 0 -3
-4 -1 0 -1 -4
-3 0 1 0 -3
0 3 4 3 0
5 8 9 8 5
>>mesh(x,y,z); (построение каркасного графика)
Для получения менее грубого графика следует сетку делать более плотной.
[x y]=meshgrid(-2:0.1:2,-3:0.1:3);
z=y.^2-x.^2;
mesh(x,y,z);
Кроме построения каркасного графика есть функция surf, которая строить каркасную поверхность, заливая каждую ее клетку цветом, который зависит от значения функции в узлах сетки.
ПРИМЕР 3. Построить график
функции ![]() .
.
[x y]=meshgrid(-2:0.2:2,-2:0.2:2);
z=sqrt(x.^2+y.^2);
surf(x,y,z);
Можно построить графики двух поверхностей в одной системе координат. Для этого, как и для плоских графиков, следует исследовать команду holdon, которая блокирует создание второго графического окна при выполнении команд surfи mesh.
ПРИМЕР 4. Построитьграфик функцииz(x,y) = ± (x2 + y2) – 1.
[x,y]=meshgrid(-2:0.2:2,-2:0.2:2);
z=x.^2+y.^2)-1;
z1=-x.^2-y.^2-1;
surf(x,y,z);
hold on
surf(x,y,z1);
Анимация
При изучении движения точки на плоскости и в пространстве можно построить график движения точки и проследить за ним. Для построения анимационного ролика существуют две функции: comet(x,y) – движение точки вдоль кривой у(х) и comet3(x,y,z) – движение вдоль пространственной кривой z(x,y).
ПРИМЕР 5. Построить
анимацию движения точки на плоскости вдоль эллипса, который параметрическое
уравнение которого имеет вид: ![]() .
.
t=0:0.001:2*pi;
x=cos(t);
y=3*sin(t);
comet(x,y);
ПРИМЕР 6. Построить
анимацию точки вдоль винтовой линии, параметрическое уравнение которой имеет
вид: 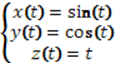 .
.
t=0:pi/500:10*pi;
comet3(sin(t),cos(t),t);
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Построить график заданной функции:
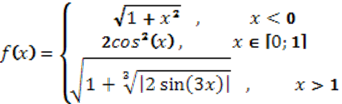 .
.
2. Выполнить построение поверхностей различного типа:
1. z(x,y) = x2 – 2y2;
2. z(x,y)=3x2 – 2 sin2(y) y2;
3. z(x,y)=3e2x x – 2 y;
4. ![]()
5. ![]()
6. ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.