Курс лекций по дисциплинам: «Теория надежности», «Надежность и диагностика технологического оборудования»

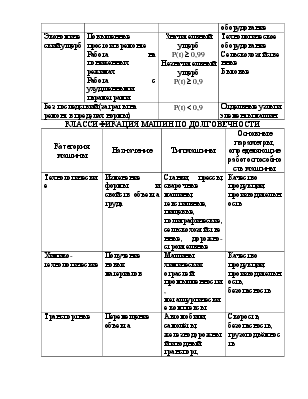
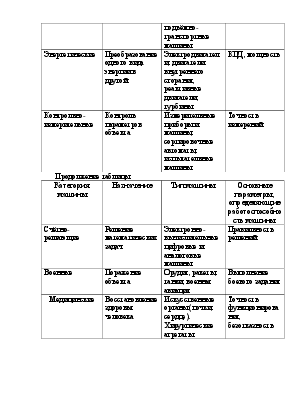
начала характеристического вектора и угла  его  наклона Dj.  Изменение  координаты  DX  при  вращении шпинделя определяет форму обработанной  поверхности  в  поперечном    сечении   (см. рисунок)   и   может   быть   оценено  одним   или   несколькими  членами

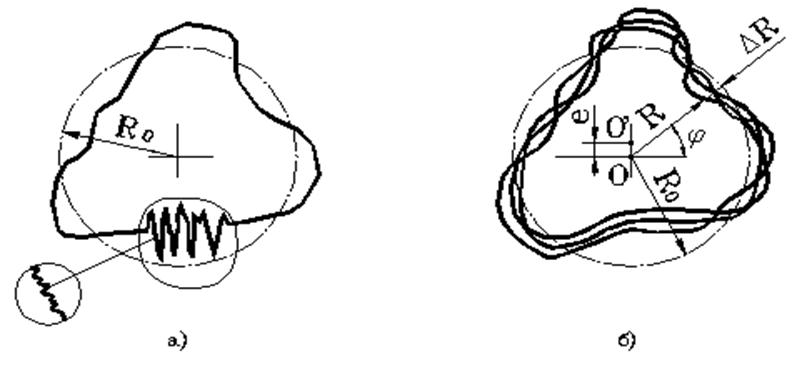
Рисунок - Связь траекторий опорных точек и формы поверхности детали: а - сечение детали, б – траектория опорной точки шпинделя разложения круговой  траектории  опорной  точки  шпинделя  в  ряд Фурье, вида:

DR(j)=C₀ + SC_k ×cos(kj+j_k) , где C_k - амплитуда k-ой гармоники; 

j_k -  начальная  фаза;

C₀  - значение погрешности размера, равное:

   .

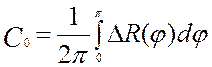Первый член разложения C₁ × cos (j + j) выражает  эксцентриситет обработанной  поверхности,  причем C₁  численно  равно  величине эксцентриситета.  Второй член ряда выражает  овальность  профиля, третий  -  трехгранку  и  т.п.  Начиная  с  k = 15 члены ряда выражают волнистость обработанной поверхности,  а  члены  ряда  с  k = 46  шероховатость  обработанной  поверхности.  Для  наглядности сведем параметры круговой траектории в таблице 1.

Таблица 1 - Выходные параметры круговой траектории ШУ

Таким образом,   область   состояния   параметров   качества шпинделя полностью определяется вектором вибрации опорной  точки, расположенной  на  базовой  поверхности  шпинделя.  Координата DZ определяет точность торцовых поверхностей,  а изменение  угла  Da влияет  на  конусность  или другие погрешности формы обработанной цилиндрической поверхности в продольном направлении (по оси Z).

Концептуальная схема,  представленная на  рисунке отражает взаимовлияние   процессов,   имеющих  место  в  трибомеханической системе ШУ при его работе.

Исходные данные                                                        Выходные данные

Конструктивные:

Внешние:                                                                                                                                               

Технологические:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ  ОБЛАСТЕЙ

 СОСТОЯНИЯ ПАРАМЕТРОВ КАЧЕСТВА ШПИНДЕЛЬНЫХ УЗЛОВ ПРИ ДЕЙСТВИИ БЫСТРОПРОТЕКАЮЩИХ

ПРОЦЕССОВ  И  ПРОЦЕССОВ  СРЕДНЕЙ СКОРОСТИ

Математическая  модель   колебаний   шпинделя   на   опорах

качения

Расчетная схема ШУ отражает следующие допущения,  принятые при  разработке  модели  колебаний шпинделя:

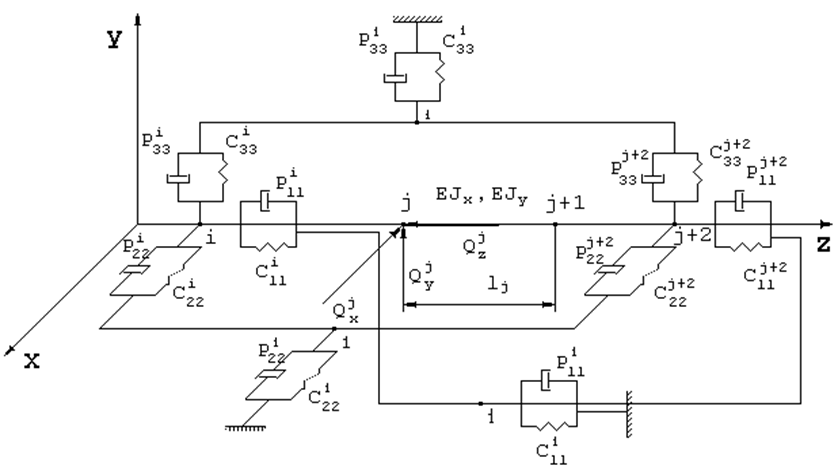
Рисунок 1 - Расчетная схема ШУ

- рассматриваются изгибные и продольные колебания  шпинделя, при   дискретизации   каждой   узловой  точке  соответствует  три обобщенных перемещения, матрица масс ШУ принимается диагональной;

- шпиндель представляется  в виде балки переменного сечения, материал которой подчиняется закону Гука  на  упруго-демпфирующих опорах   с   вязким   трением,   величина,   силы   демпфирования пропорциональны    относительной    скорости    вибрации    колец подшипников;          - корпус ШУ представлен в  виде  эквивалентного  стержневого конечного элемента;

- обрабатываемая  деталь  представлена  в   виде   конечного элемента - стержня;

- устройство  зажима  заготовки   моделируется   посредством добавления  жесткости  и демпфирования устройства в узле стыковки обрабатываемой детали и шпинделя;

- источниками вибровозмущений являются дефекты  изготовления и   сборки   подшипников,   а   также   дисбалансы   шпинделя   и смонтированных на них деталей;

- ременная    передача,   передающая    вращение   шпинделю, рассматривается как упругая связь;

- учитывается   наличие   различного   рода   отверстий, шпоночных  пазов и т.п.  в теле шпинделя посредством неодинаковых осевых моментов инерции;

- вибровозмущения,  генерируемые приводом шпиндельного узла, учитываются  посредством  задания  возмущения  от привода в узле, расположенном в месте крепления приводной передачи;

- сила резания задается в координатах  относительно  базовой поверхности шпинделя.

Модель ШУ  составляем  на  основе  метода конечных элементов.  Шпиндель при этом разбивается на  n  конечных элементов,  которые  связаны  между  собой  в узлах.  Перемещения узлов, каждый из которых при принятых допущениях имеет 5 степеней свободы,  принимаются  за  обобщенные  координаты системы.  Общее число степеней свободы при этом равно N = 5 (n + 1).

Выражения для  возмущающих  сил  от  подшипников  -  F_i^П ,  соответствующих выбранным обобщенным координатам можно  представить  в  следующем виде :

F_iⁿ = -F_i^упр - F_i^демп + F_i^ц + F_i^т ,  i = 1, ...5 , где F_i^упр  -  силы  и моменты,  обусловленные упругими свойствами подшипника; 

F_i^ц -  возмущающие  силы  и  моменты,  обусловленные действием центробежных сил на тела качения;

F_i^т -  силы   и   моменты,   обусловленные   технологическими погрешностями;

F_i^демп - демпфирующие силы и моменты.

Значения спектральных   амплитуд    возмущающих    сил    от погрешностей  изготовления шарикоподшипника  и частот, на которых они проявляются, приведены в табл.1.

Таблица 1- Амплитудный спектр радиальных вибровозмущений, генерируемых шарикоподшипником

В табл.1 n - число тел качения; 

t - угол контакта; 

  s - геометрический осевой натяг; 

K_z - осевая жесткость шарикоподшипника;

 w_н,w_в,w_ш - частоты вращения  сепаратора  относительно  наружного, внутреннего кольца  и  шариков  вокруг  собственной оси;   

 p - номер гармоники разложения в ряд Фурье радиуса шариков; 

a_p - наиболее  вероятное значение  амплитуды p - й гармоники радиуса шарика для партии ШП;

 l,x,a_l,a_x - номера и амплитуды гармоник приведенных  погрешностей макрогеометрии наружного и внутреннего колец.

Геометрическая интерпретация гармоник  погрешностей  дорожек качения колец, дается на рис. (2) на примере наружного кольца.

Рис.2 - Геометрическая интерпретация  гармоник  погрешностей

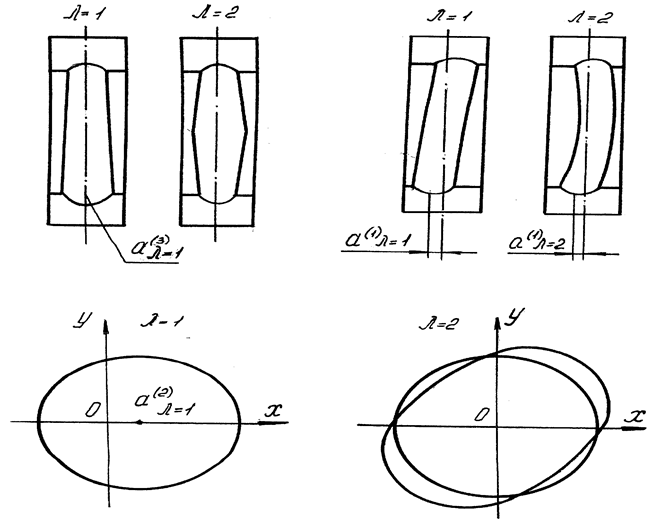
дорожек качения колец шарикоподшипника

Для расчетного  определения амплитудных спектров погрешностей колец и тел  качения  можно  использовать  метод,  основанный  на аппроксимации  спектров  гиперболическими  линиями регрессии. Характеристики дефектов сборки  шарикоподшипников, даны в табл. 2.

Таблица 2 - Дефекты сборки шарикоподшипников

Обозначения: R_q- расстояние от оси вращения подшипника