Исследование функций и построение графиков. Вариант № 1, страница 3

Точка персечения с осью ОУ: х = 0, y = 0;

Точка персечения с осью ОХ: у = 0, х = 0.

2.  Свойства функции:

Функция ни четная, ни нечетная.

Функция не периодическая. Функция общего плана.

3.  Точки разрыва:

Разрыв II рода

Имеется 1 точка разрыва x = –1 и  имеется 1 вертикальная асимптоты

  

4.  Исследование по первой производной:

 

Определим критические точки:

 – критическая точка х = 0;

 – поскольку критическая точка х = -1 не входит в D()

.

 

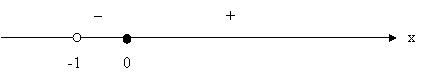Получаем в точке х = 0 гладкий миниум.

5.  Исследование по второй производной:

Определим критические точки:

 – критических точек нет;

При несуществующем, критическая точка х = –1, но поскольку х = -1 .

 точек подозрительных на точку прегиба у функции нет.

6.  Определение ассимптот:

·  Вертикальные ассимптоты:

Вертикальные ассимптоты функции будут в точке разрыва имеем 1 вертикальную ассимптоту: х = –1.

·  Наклонные ассимптоты:

, где

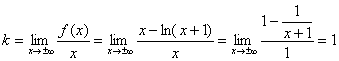
наклонных ассимпотот нет.

7.  График функции:

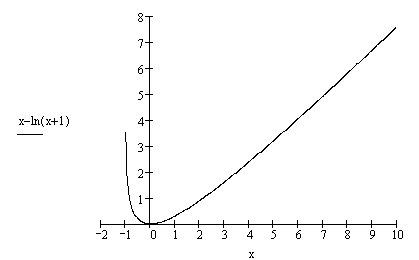
Задание 3.  Через точку Р(1;4) провести прямую так, чтоб сумма длин положительных отрезков, отсекаемых на координатных осях была наименьшей.

Решение:

у

4

x