Прямоугольные и цилиндрические резонаторы

Добротность нагруженного резонатора

Q=×f0×m×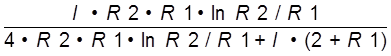(2lnR2/R1+lp/4(1/R2+1/R1))

Резонансная частота нагруженного резонатора

 

× Сэ

wо= -Хсв/2Lэ + 1/   Lэ×Cэ   ×      1+          4Lэ

Коаксиальный резонатор с зазором

Коаксиальный резонатор с зазором показан на рисунке 

 

1                                                                                                                                                                                               

 

                                                                                                                                                                                                    

                                                                                                             C1                                        

                                                                                                                        

r

                                                                                                                       

 

1                                                                                    l  

                                                                                                                         

d                           l      

Резонатор состоит из двух частей: отрезка коротко замкнутой линии, длиной меньшей l/4, входное сопротивление которой  в сечении 1-1 имеет индуктивный характер, и конденсатора, образованного торцом внутреннего проводника в сечении 1-1 и стенкой резонатора. Перестройка резонатора осуществляется изменением l и d одновременно.

Наиболее просто условие резонанса записывается для сечения 1-1.

j×Zв× tg( ×l)+ 1/j×wo×C1=0   ,     или

ctg wo×l/C = wo×C1×Zв           ,       где С- скорость света

При плоском зазоре без учета краевых эффектов емкость зазора равна

С1= e 0×l/d= e 0×p×/d

отсюда легко определить l

l= l0/2×p×[arcсtg(wo×С1×Zв)+ p×p]  , где при р=0 lмин соответствует главному значению арккотангенса.

Преимущество обычного коаксиального резонатора – линейная зависимость резонансной частоты от длины резонатора.

Преимущество резонатора с зазором – простая перестройка частоты в широком диапазоне частот и малые размеры (близкие к l=l/4). Однако имеется и существенный недостаток – частотная зависимость резонансной частоты от d нелинейная, особенно при малых значениях d.

Прямоугольные резонаторы.

Прямоугольный резонатор представляет собой закороченный с обеих сторон отрезок прямоугольного волновода.

Резонансная длина волны такого резонатора определяется как

                      1                    Р         2

lрез = 1/      lкр   +   (     2l      )  , или

                             m      2          n        2          p         2

     lрез = 2/          a          +      b              +    l                     

Структура волн определяется индексами m, n и p и колебания в резонаторах обозначается как Нmnp и Emnp.

Волна Н101

 

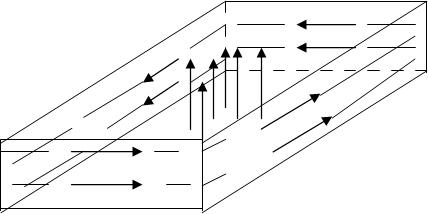Как видно из рисунка электрическое поле максимально в центре резонатора, а магнитное у его стенок. Электромагнитное поле в резонаторе обладает всеми свойствами стоячей волны. Составляющие магнитного поля имеют фазовые сдвиги p/2 по отношению к составляющим магнитного поля. Каждые четверть периода вся запасенная энергия переходит поочередно в электрическую и магнитную. Фазовые изменения происходят следующим образом: все составляющие электрического поля одновременно уменьшаются по амплитуде от своего максимального значения до нуля, а затем векторы электрического поля меняют направление на противоположное и увеличиваются от нуля до максимального значения. Аналогично ведут себя и магнитные составляющие, но с запаздыванием по времени на четверть периода.

             Волна Е111                                                                                                                       Волна  Е110                

   .        .          .          .        .   

                                                                        

                                            Z                                                                                  z   

При любом типе колебаний в прямоугольном резонаторе только один из трех индексов  m, n или р может быть равен нулю. Выражение для добротности любого резонатора можно записать в виде

                         2

  1    =  1 ×    l          a+      R    × ep

 Qo         p     lв                 Zв×l                , где   a- постоянная затухания для соответствующего резонатору волновода типа волны Еmn или Нmn1 , eо=1, если р=0 и  eр=2, если р=1,2,3,…

Так как в общем случае

                    ó          2

õ  Hm        dV

   Qо= 2/D×    V

                              ó                2         

                    õ    Hmt        dS                     ,

S

то вводя усредненные значения квадрата напряженности магнитного поля

()V  и ()S по объему и по поверхности, получим

Qo= 2V/DS× ()V/()S

из последнего выражения можно сделать следующие выводы:

-  добротность резонатора определяется отношением его объема к поверхности,

-      добротность зависит от типа колебаний, так как  ()V   и  /()S зависят от  структуры составляющих векторов магнитного поля,

-     добротность зависит от проводимости материала, из которого изготовлен резонатор.

Цилиндрические резонаторы.

Цилиндрический резонатор представляет собой закороченный с обеих сторон отрезок круглого волновода.

Резонансная длина волны цилиндрического резонатора

                     U; U          2              P      2    

l0= 2/                                 + 

                      p                           l                         ,

 

где U;U   - означает, что для волн типа Е следует брать U, а для волн типа Н брать U    .

          значение U и U  , как известно из теории цилиндрических волновод определяются из уравнений