Петербургский Государственный Университет Путей Сообщения
Кафедра: “Инженерная гидрология”
Задание №1, вариант №1
Выполнил: студент группы
МТ-802м-В Даниленко Р.И.
Проверил:
Санкт – Петербург 20.12
Хронологический ряд максимальных расходов воды в реке А.
Для выбранного варианта расчетов из прил.1 берётся ряд максимальных расходов воды в реке А продолжительностью n=31:
|
233 |
|
105 |
|
170 |
|
205 |
|
123 |
|
222 |
|
143 |
|
180 |
|
210 |
|
128 |
|
225 |
|
149 |
|
192 |
|
116 |
|
174 |
|
280 |
|
96 |
|
147 |
|
183 |
|
63 |
|
148 |
|
215 |
|
120 |
|
152 |
|
176 |
|
135 |
|
252 |
|
71 |
|
168 |
|
133 |
|
201 |
1. Расположим числа данного ряда в возрастающем порядке:
|
280 |
|
252 |
|
233 |
|
225 |
|
222 |
|
215 |
|
210 |
|
205 |
|
201 |
|
192 |
|
183 |
|
180 |
|
176 |
|
174 |
|
170 |
|
168 |
|
152 |
|
149 |
|
148 |
|
147 |
|
143 |
|
135 |
|
133 |
|
128 |
|
123 |
|
120 |
|
116 |
|
105 |
|
96 |
|
71 |
|
63 |
2. Определим размах (амплитуду) колебаний максимальных расходов в ряду наблюдений:
Q = Qmax - Qmin = 280 – 63 = 217 м3/с.
3. Вычислим количество интервалов по эмпирической формуле:
k = 5 * ℓg n = 5 * ℓg 31 = 5 * 1.49 = 7.46.
Округлив значение до целого числа, примем k = 7.
4. Вычислим размер интервала с точностью до 0,1:
Δ Q = Q / k = 217 / 7 = 31 м3/с.
5. Найдем количество членов ряда ni , входящих в каждый интервал (абсолютную частоту появления), и относительную частоту появления 100 * ni / n , % (табл.1).
Например, во второй интервал – от 240,9 до 296,8 м3/с – входят 4 расхода из ряда наблюдений, т.е. абсолютная частота их появления в ряду наблюдений составляет ni = 4, а относительная – 12,9%. Каждый расход включается в интервал только один раз. При определении границ последнего интервала максимальное значение расхода следует принять равным наибольшему числу из ряда наблюдений.
6. Построим гистограмму распределения частоты появления (повторяемости) максимальных расходов воды (рис. 1).
7. Проведем суммирование относительных частот, начиная от наибольшего расхода (снизу вверх), и определим вероятность превышения (обеспеченность) каждого интервала ряда наблюдений pi = (∑ ni / n) * 100,% (табл. 1).
8. Построим ступенчатый график и плавную кривую обеспеченности максимальных расходов воды, которая должна проходить через середины интервалов (рис. 2). По оси абсцисс откладываются обеспеченности от 0 до 100% (масштаб: 1 см – 5 или 10%), по оси ординат – интервалы максимальных расходов (масштаб: 1 интервал – 2 или 1 см).
ni
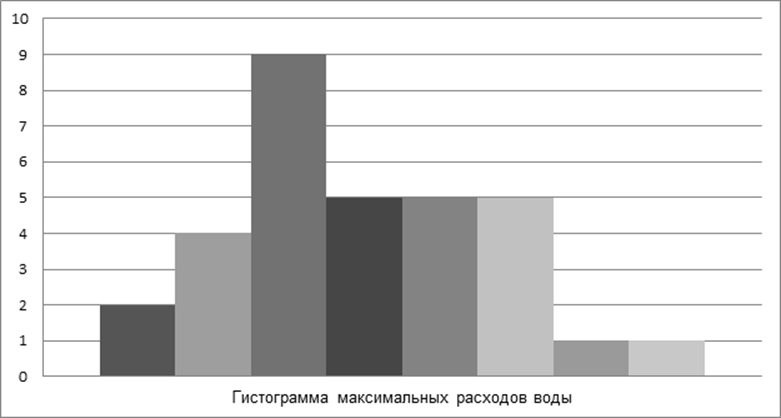
Максимальные расходы воды, м3/с
Рис.1 Гистограмма максимальных расходов воды
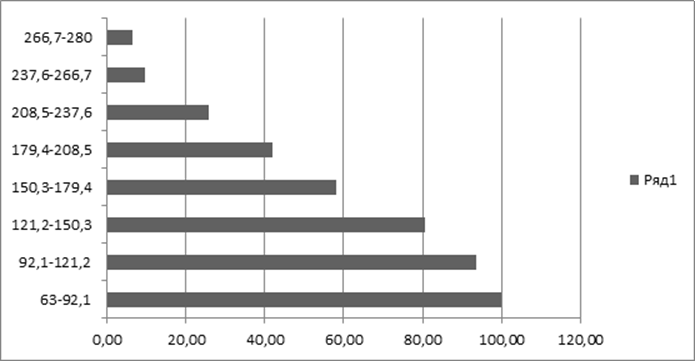
 |
Обеспеченность, %
Рис.2. Гистограмма и кривая обеспеченности максимальных расходов воды
По кривой обеспеченности определим, что числу 576 в данном ряду соответствует обеспеченность (вероятность превышения)
p = 100% * 1 / 32 = 3,1 %.
Таблица 1
|
Столбец1 |
Столбец2 |
Столбец3 |
Столбец4 |
Столбец5 |
|
№ интервалов |
Интервал (ΔQi) м^3/c |
ni |
100%*ni/n, % |
Pi, % |
|
1 |
63-92,1 |
2 |
6,45 |
100,00 |
|
2 |
92,1-121,2 |
4 |
12,90 |
93,55 |
|
3 |
121,2-150,3 |
7 |
22,58 |
80,64 |
|
4 |
150,3-179,4 |
5 |
16,13 |
58,06 |
|
5 |
179,4-208,5 |
5 |
16,13 |
41,93 |
|
6 |
208,5-237,6 |
5 |
16,13 |
25,80 |
|
7 |
237,6-266,7 |
1 |
3,23 |
9,68 |
|
8 |
266,7-280 |
2 |
6,45 |
6,45 |
|
∑ |
31 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.