Определение размаха (амплитуды) колебаний максимальных расходов воды в реке, страница 2

9. Определим среднеарифметическое значение ряда по формуле:

Q_ср  =  ∑ Q_i / n  5115 / 31 =  165 м³/с                  

где     ∑ Q_i  - сумма значений ряда, м³/с;

n =31 – число членов ряда.   

Вычислим для каждого члена значения модульного коэффициента К_i

                                 К_i = Q_i / Q_cр  (1)

где – Q_i – максимальный расход воды в i –ый год наблюдений;

Q_cр – среднеарифметическое значение ряда наблюдений.                                               

Последовательно просуммируем (нарастающим итогом) значения (К_i – 1) и по результатам расчетов (табл. 2) построим разностную интегральную кривую ∑(К – 1) = f(T) для рассматриваемого хронологи-ческого ряда наблюдений (рис. 3). Для лучшего анализа проведем сглаживающую кривую.       

На построенном сглаженном графике выделим фазы маловодных и многоводных лет. Количество маловодных фаз (спадов кривой) составило 3, многоводных (подъемов кривой) – 2.  Продолжительность многоводных  маловодных лет в периоде наблюдений (1972…2002 гг.) оказалось примерно равной.

Таким образом, можно считать рассматриваемый ряд наблюдений за стоком нерепрезентативным.                                          

Таблица 2

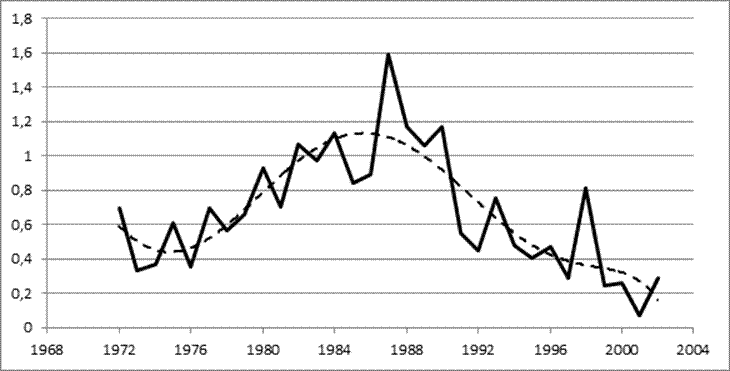
Рис.3 Разностная интегральная кривая стока воды