Изучение фигур по методу Лиссажу и исследование биения при помощи осциллографа, страница 2

Фигуры Лиссажу  ^__ замкнутые траектории точки, одновременно совершающей гармонические колебания в двух взаимно перпендикулярных направлениях. Фигуры Лиссажу основаны на сложении взаимно перпендикулярных гармонических колебаний одинаковой частоты.

3) Основные физические законы.

а) Фигуры Лиссажу отвечают следующему свойству: отношение частот гармонических сигналов  равно отношению максимального числа точек пересечения данной фигуры с вертикальной и горизонтальной осями .

б) Амплитуда биений зависит  от  времени

    , где

А_р- амплитуда результирующего колебания

А - амплитуда колебания (м)     (А₁=А₂=А амплитуды колебаний одинаковы)

  t=0…nT

4)Теоретически ожидаемый результат.

1)Определение частоты синусоидальных сигналов по методу фигур Лиссажу.

Метод Лиссажу: В результате сложения взаимно перпендикулярных колебаний одинаковых частот (или частот в отношениях ½, ¼, 2/3, 2/5) на экране осциллографа можно наблюдать фигуры Лиссажу. В случае если взаимно перпендикулярные колебания одинаковых частот на экране можно фигуру наблюдать плавно переходящие от круга через эллипс к прямой и обратно.

2

Для фигур Лиссажу справедливо: отношение частот гармонических сигналов  равно отношению максимального числа точек пересечения данной фигуры с вертикальной и горизонтальной осями  .

 

2)Исследование биений.

Строим теоретически предполагаемый график

Изи Dw =  2p/Т_б следует, что Dw=const . t – увеличивается, значит  угол  будет увеличиваться, а Cos - убывать от значения 1 до –1.

 Анализируя формулу,  получаем что она соответствует  y=kx+b , при том, что  k=1, а  b=0. Следовательно, график функции будет представлять прямую линию (биссектрису I –й и III -й четвертей прямоугольной системы координат).

Теоретически предполагаемый график:

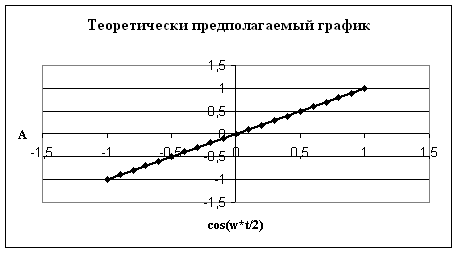Из графика следует вывод, что амплитуда зависит от  прямо пропорционально.

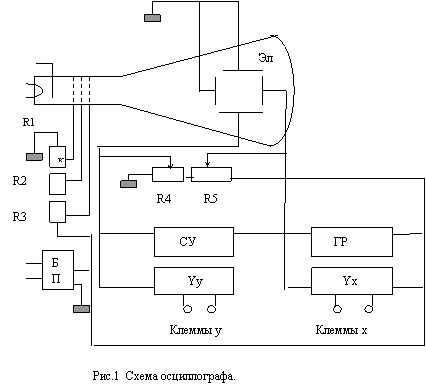
3. Схема установки

 

4. Основные расчетные формулы

1.Получение фигур Лиссажу.

  

, где

 f_x и f_y -  частоты гармонических сигналов   

n_x и n_y-  максимальное число точек  пересечения данной фигуры с вертикальной  и горизонтальной  осями.