Оптимальное распределение заданной суммарной мощности компенсирующих устройств между цехами промышленного предприятия

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра электроснабжения

КОНТРОЛЬНАЯ РАБОТА №2

Дисциплина «Оптимизационные задачи электроэнергетики»

Студент: Захаров П.Ю.

Специальность: 140211

Курс: 3

Шифр: 0101051993

г. Санкт-Петербург

2011

Задача 1.

Электроснабжение n цехов промышленного предприятия выполнено по радиальной схеме от шин U = 10 кВ (рис. 1). Заданы реактивные нагрузки цехов Qi и активные сопротивления радиальных линий ri (i = 1, 2, ... n). Требуется оптимально распределить заданную суммарную мощность компенсирующих устройств Qk между цехами. Критерий оптимальности -  минимум суммарных потерь активной мощности в схеме.

Исходные данные для решения задачи :

.

      Дано:                                         

r₁ =  0,3 Ом                                       

r₂ =  0,5 Ом

r₃ = 0,4  Ом                                                                                                                

Q₁ = 1800 квар                                                                             

Q₂ = 1000 квар                                                                       

Q₃ = 3300 квар                     

Q_k = 5100 квар

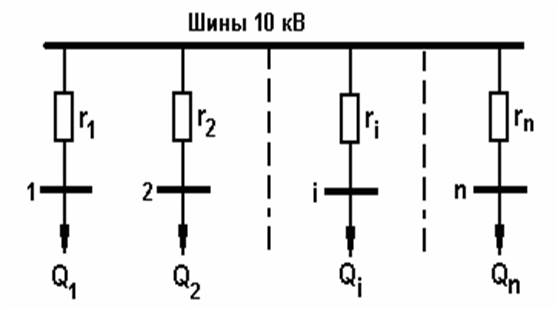рис.1

Решение.

Потери активной мощности в радиальной схеме электроснабжения от реактивных нагрузок Q_i при установке у каждой нагрузки компенсирующего устройства мощностью Qki определяются выражением:

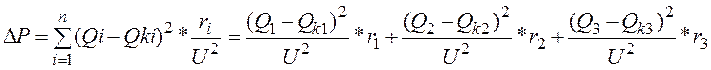(1)

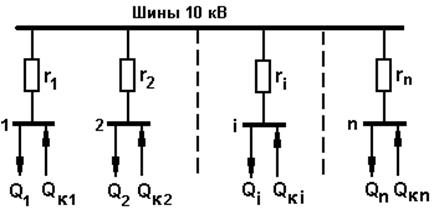                                          . Размещение компенсирующих устройств в радиальной схеме электроснабжения

Необходимо найти минимум  D Р при условии (ограничении):

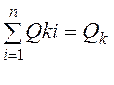или Q_k1+Q_k2 +Q_k3 = Q_k = 4100 квар   5100           (2)

Следуя методу неопределенных множителей Лагранжа, вместо минимума функции (1) при ограничении (2) будем искать минимум функции Лагранжа. Запишем функцию Лагранжа (3) в виде:

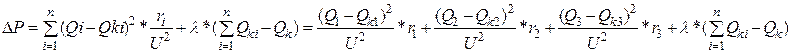
где  - неопределенный множитель Лагранжа.

В точке минимума функции ее частные производные по всем переменным равны нулю, т.е.:

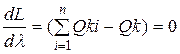
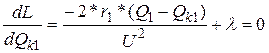
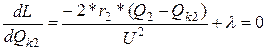                                  (4)

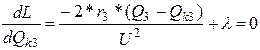
Вычислим частные производные от функции Лагранжа по переменным  и Q_ki, при этом решение системы линейных уравнений (4) даст искомые значения переменных Q_ki:

;                  ;

;                                           ;

;                                              ;

 .                                           .

;

;

;

.

;

;

;

;

       

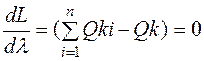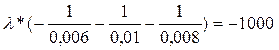Определим реактивные нагрузки в каждой из отходящих линий (1,2,3) после установки компенсирующих устройств мощностью Q_k1, Q_k2 , Q_k3 соответственно:

                                                                         

На основании полученных данных можно вывести отношение, согласно которому частное реактивных мощностей после компенсации, двух линий обратно пропорционально частному сопротивлений этих двух линий, то есть: 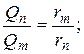                                например

Задача 2.

Схема электроснабжения  цеха промышленного предприятия выполнена магистральным шинопроводом от шин U = 0,4 кВ цеховой подстанции     (рис. 7). Вдоль шинопровода расположены нагрузки, реактивные составляющие которых равны Q_i, а активные сопротивления участков между точками подключения нагрузок равны г_i (i=l,2,3). Определить в какой из точек 1,2,3 подключение компенсирующего устройства заданной мощности Q_k обеспечит минимум потерь активной мощности от протекания реактивных нагрузок. Исходные данные для решения задачи приведены ниже.

      Дано:                   

                                                                               

r₁ =  0,003 Ом                                           

r₂ =  0,005 Ом      

r₃ = 0,004 Ом                                                                                                 

Q₁ = 300 квар                                                                        

Q₂ = 400 квар                                                                                                     

Q₃ = 300 квар                                                                                                                           

Q_k = 700 квар

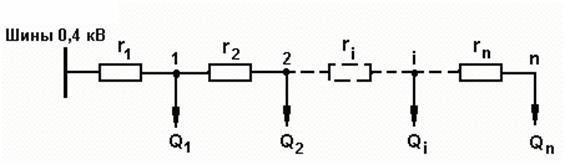Рис. 7 Магистральная схема электроснабжения

Решение.

В магистральных схемах внутрицехового электроснабжения, как правило, выбирают одну точку подключения компенсирующего устройства заданной мощности Q_k. В рассматриваемой задаче имеется 3 возможных точек подключения компенсирующего устройства Q_k. Это точки 1, 2, 3.

Выбор точки подключения компенсирующего устройства может быть выполнен различными методами, два из которых рассмотрим ниже.

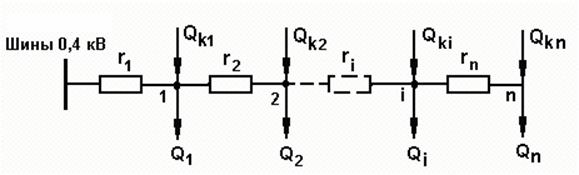
Рис. 8 Размещение компенсирующих устройств в схеме

Метод простого перебора возможных вариантов.

В этом случае компенсирующее устройство мощностью Q_k поочередно подключаем к каждой  i-ой точке магистрального шинопровода. В каждом  i-ом случае рассчитываем потокораспределение реактивных мощностей в ветвях магистральной схемы и определяются суммарные потери активной мощности по выражению:

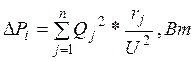                           (1)

где Q_j - поток реактивной мощности в  j-ой ветви магистрального шинопровода;

r_j  - сопротивление j-ой ветви магистрального  шинопровода.

1.  Установка компенсирующего устройства в точке 1.

2.   Установка компенсирующего устройства в точке 2.

3.   Установка компенсирующего устройства в точке 3.

На основании результатов проведённого расчета можно сделать вывод, что наиболее целесообразным местом подключения компенсирующего устройства будет точка 2, так как в этом случае потери активной