4. Уравнение Бернулли для элементарной струйки идеальной жидкости. Аналитическое выражение, геометрический и энергетический смысл понятий: гидростатический, пьезометрический, скоростной и полный напоры.
Отработка второго учебного вопроса включает в себя заслушивание и обсуждение докладов по темам:
1. Что понимается под термином «поток жидкости»; гидравлические элементы потока; понятие «средняя скорость потока жидкости»?
2. Уравнение Бернулли для потока реальной жидкости. Аналитическое выражение, физическая сущность. Энергетические условия ускорения и замедления движения жидкости. Методика применения уравнения Бернулли для решения инженерных задач.
После заслушивания и обсуждения докладов отработать приемы применения уравнения Бернулли для решения следующих задач.
Задача 1. Составить уравнение Бернулли для гидравлической системы (рис. 3), включающей в себя открытый резервуар, заполненный жидкостью до определенного уровня 1–1. Жидкость вытекает через открытое сечение 2–2 в атмосферу с давлением Р0. Условную плоскость сравнения принять на уровне 0–0.
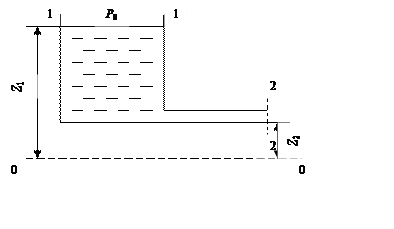
Рис. 3
Задача 2. Составить уравнение Бернулли для гидравлической системы (рис. 4), состоящей из наклонного сужающегося трубопровода, через который движется жидкость. Уровень жидкости в центре входного сечения трубопровода Z1, а выходного Z2. В трубопроводе установлены пьезометрические трубки, уровни жидкости в которых по отношению к Z1 и Z2, составляют соответственно h1 и h2.
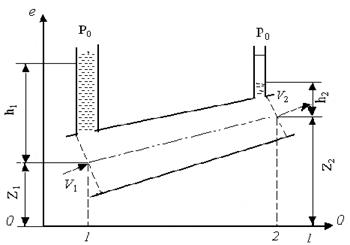
Рис. 4
Вопросы для самопроверки
1. Как изменится скорость движения жидкости при проходе через сужающийся трубопровод?
2. Как изменится скорость движения жидкости при проходе через расширяющийся трубопровод?
3. Как изменится давление в жидкости при проходе через сужающийся и расширяющийся трубопроводы?
4. Как определить среднюю скорость потока жидкости, вытекающего из трубопровода, если известно его живое сечение?
Практическое занятие 4. Режимы движения жидкости
Цели занятия: изучить природу и физическую сущность образования различных режимов движения жидкости: ламинарного и турбулентного; уяснить законы распределения скорости жидкости при ламинарном и турбулентном движении, зависимость режима движения от числа Рейнольдса; усвоить порядок определения потерь на трение по длине потока и получить практику их расчета.
Задание на самостоятельную подготовку к занятию:
1. По материалам лекции 5 «Режимы движения жидкости» и учебного пособия [1] (с. 67–79) изучить основные виды движения жидкости, их природу и физическую сущность, влияние на формирование потерь на трение потока по его длине.
2. Быть готовыми ответить на следующие контрольные вопросы:
· Какие существуют режимы движения жидкости, их отличия и характеристики?
· Число Рейнольдса: формула, входящие в нее величины, физический смысл.
· Формирование вязкого пограничного слоя при различных режимах движения жидкости.
· Формула Дарси для расчета потерь на трение для ламинарного режима движения жидкости.
Порядок проведения занятия
Занятие включает в себя проверку подготовленности студентов к занятию и отработку двух учебных вопросов:
1. Два режима движения жидкости.
2. Определение режима движения вязкой жидкости и расчет коэффициента потерь на трение по длине.
По первому учебному вопросу заслушиваются доклады студентов с изложением и записью рассматриваемых положений на доске.
Темы докладов
1. Основное уравнение равномерного движения жидкости.
2. Распределение скоростей потока по сечению при ламинарном режиме.
3. Вывод формулы Дарси для определения гидравлических потерь на трение по длине и ее анализ.
4. Формулы для расчета коэффициента потерь на трение по длине для турбулентного режима движения жидкости.
В обсуждении докладов принимают участие все студенты путем изложения необходимых уточнений и дополнений.
При отработке второго учебного вопроса решить задачи по указанию преподавателя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.