Расчётное задание по дисциплине «Теория вероятности и математическая статистика», страница 4

        

         Доверительный интервал для дисперсии:

        

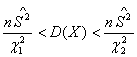
         Тут и - критерии распределения  Пирсона, значение который составляет  и  при уровне значимости  и .

        

         Выдвигаем гипотезу о законе распределения

        

        

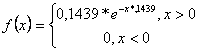
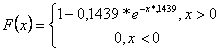
         Проверка статистических гипотез распределения случайной величины

Цель:                   Выучить критерии согласия, научиться проверять гипотезы о законе распределения случайной величины с помощью критериев Пирсона и Колмогорова при анализе статистических данных.

Ход работы.

         Критерий Пирсона.

         При использовании критерия Пирсона за меру несоответствия принимается величина , вычисленная по формуле:

        

         Тут  - число интервалов

          - частота попадания в интервал

          - вероятность попадания случайной величины в интервал, вычисленная по проверяемому закону распределения.

         Вероятность попадания величины в заданный интервал при показательном распределении равна.

        

Границы интервала	[0.00; 3.86]	(3.86; 7.72]	(7.72; 11.58]	(11.58; 15.44]	(15.44; 19.30]	(19.30; 23.16]	(23.16; 27.02]	(27.02; 30.88]	(30.88; 34.74]	(34.74; 38.60]
Частота попадания	41	23	20	6	6	1	1	0	1	1
Вероятность попадания	0.42611	0.24454	0.14034	0.08054	0.04622	0.02653	0.01522	0.00874	0.00501	0.00288
	0.06090	0.08645	2.53627	0.52381	0.41077	1.02957	0.17919	0.87363	0.49591	1.76321