Расчётное задание по дисциплине «Теория вероятности и математическая статистика», страница 3

         По данным полученного вариационного ряда построим гистограмму – статистический аналог плотности распределения (рисунок 1) и график эмпирической функции распределения (рисунок 2).

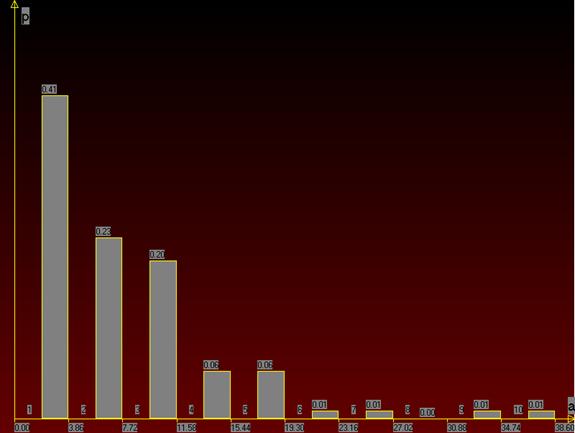
(рисунок 1)

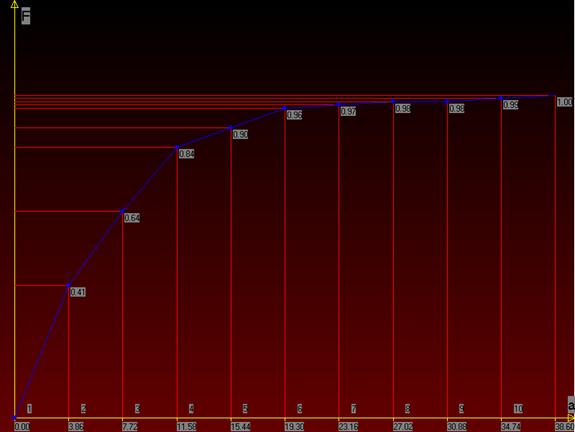
(рисунок 2)

         Анализируя гистограмму и график эмпирической функции распределения можно выдвинуть гипотезу о показательном законе распределения.

         Параметрическое оценивание закона распределения случайной величины.

Цель:                   Выучить методы параметрического оценивания законов распределения случайной величины, научиться применять эти методы при анализе статистических данных.

Ход работы.

         Параметрический способ оценивания распределения случайной величины состоит в определении неизвестных параметров закона распределения, тип которого неизвестен или предполагается.

         Проведём оценку параметров для показательного распределения, гипотезу о котором мы выдвинули на предыдущем этапе. По условию доверительная вероятность , уровень значимости

         Оценка параметра для показательного распределения вычисляется по формуле:

        

         За оценку мат. Ожидания берут среднее арифметическое эл-тов выборки.

        

где

        

         За оценку дисперсии берут исправленную выборочную дисперсию:

               

         Результаты вычислений параметров показательного закона распределения

        

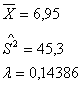
         Доверительный интервал математического ожидания:

        

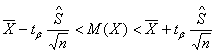
         Тут  =1,9842 – критическая точка распределения Стьюдента. Определяется по таблице для числа степеней свободы  и уровня значимости .