Расчётное задание по дисциплине «Теория вероятности и математическая статистика», страница 2

(Табл.1)

         1. Непараметрические методы оценивания закона распределения случайной величины.

Цель:                   Выучить непараметрические методы оценки законов распределения случайной величины по выборке, научиться применять эти методы при анализе статистических данных.

Ход работы.

          Вычислим интервал вариационного ряда.

 

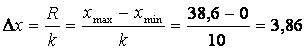          где -число интервалов

          -минимальный элемент выборки

          -максимальный элемент выборки

          -размах выборки

         Для размера выборки n=100 наиболее оптимальным является число интервалов k=10.

         Нижняя граница:

        

         Каждая следующая:

        

         Последняя (верхняя) граница:

        

         Далее элементы распределяют на интервалы, причём граница интервала относится к тому интервалу, который расположен слева от этой границы. Исключение – нижняя граница, она относится к первому интервалу.

         Далее рассчитаем частоту  и относительную частоту (частость)  попадания элементов выборки в интервалы. А для построения стахостического аналога плотности распределения случайной величины, рассчитаем плотность распределения  для каждого интервала.

        

Номер интервала	1	2	3	4	5	6	7	8	9	10
Границы интервала	[0.00; 3.86]	(3.86; 7.72]	(7.72; 11.58]	(11.58; 15.44]	(15.44; 19.30]	(19.30; 23.16]	(23.16; 27.02]	(27.02; 30.88]	(30.88; 34.74]	(34.74; 38.60]
Частота попадания	41	23	20	6	6	1	1	0	1	1
Частость попадания	0.41	0.23	0.20	0.06	0.06	0.01	0.01	0.00	0.01	0.01
Предст-ль интервала	1.93	5.79	9.65	13.51	17.37	21.23	25.09	28.95	32.81	36.67
Плотность попадания	0.1062	0.0596	0.0518	0.0155	0.0155	0.0026	0.0026	0.0000	0.0026	0.0026