выбрать наибольшее из полученных.
V (0 , 0 , 0 ,1 )
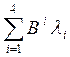 =
2*10-3;
=
2*10-3;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}= (
-(Bi)2]
}= (![]() *0,81+
*0,81+![]() *0,81) =1,62*
*0,81) =1,62*![]()
2 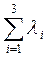
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (0 , 0 , 0 ,1 )= 1,473*10-2
V (0 , 0 , 1 ,0 )
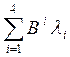 = 0;
= 0;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
} = (
-(Bi)2]
} = (![]() *1,01+
*1,01+![]() *1,01 +4*
*1,01 +4*![]() ) = 2,02*
) = 2,02*![]()
2 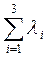
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (0 , 0 , 1 ,0 )= 1,273*10-2
V (0 , 0 , 1 ,1 )
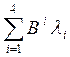 =
2*10-3;
=
2*10-3;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=2,02*
-(Bi)2]
}=2,02*![]()
2 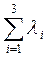
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (0 , 0 , 1 ,1 )= 1,473*10-2
V (0 , 1 , 0 ,0 )
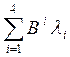 =
0,9*10-2;
=
0,9*10-2;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}= (
-(Bi)2]
}= (![]() *0,81*(1+4*10-3)+4*
*0,81*(1+4*10-3)+4*![]() )=85,324*
)=85,324*![]()
2 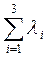
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (0 , 1 , 0 ,0 )= 0,933*10-2
V (0 , 1 , 0 ,1 )
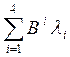 =
0,9*10-2+2*10-3+0,396*10-5;
=
0,9*10-2+2*10-3+0,396*10-5;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=
-(Bi)2]
}=![]() *0,81*(1+4*10-3)-
0,44*0,81*10-7(2+0,44*10-3)
*0,81*(1+4*10-3)-
0,44*0,81*10-7(2+0,44*10-3)
2 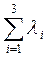
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (0 , 1 , 0 ,1 )= 1,1*10-2+0,396*10-5+0,9*10-2*(1,004-g*0,88*10-3)1/2
V (0 , 1 , 1 ,0 )
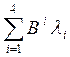 =
0,9*10-2;
=
0,9*10-2;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=
-(Bi)2]
}=![]() *1,01*(1+4*10-3)+10-7
(0,713)+4*
*1,01*(1+4*10-3)+10-7
(0,713)+4*![]()
2 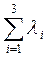
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (0 , 1 , 1 ,0 )= 0,9*10-2+10-2*(0,846+g*0,713*10-3)1/2
V (0 , 1 , 1 ,1 )
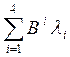 =
1,1*10-2+0,396*10-5;
=
1,1*10-2+0,396*10-5;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=
-(Bi)2]
}=![]() (0,81+3,953*10-3+2,852*10-6)+
10-4*(0,162+4,68*10-3+
(0,81+3,953*10-3+2,852*10-6)+
10-4*(0,162+4,68*10-3+
+6,25*10-6+3,47*10-9+0,62*10-12)
2 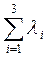
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (0 , 1 , 1 ,1 )= 1,1*10-2+0,396*10-5+10-2 *(0,81+3,953*10-3+2,852*10-6+ +g*(0,162+4,68*10-3+6,25*10-6+3,47*10-9+0,62*10-12)1/2
V (1 , 0 , 0 ,0 )
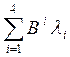 =
0,9*10-2;
=
0,9*10-2;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}= (
-(Bi)2]
}= (![]() *0,81+
*0,81+![]() *4)=85*
*4)=85*![]()
2 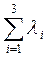
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (1 , 0 , 0 ,0 )= 0,931*10-2
V (1 , 0 , 0 ,1 )
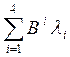 =
1,1*10-2+0,396*10-5
=
1,1*10-2+0,396*10-5
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}= (0,9*10-2*(0,87 g+1))/ g2
-(Bi)2]
}= (0,9*10-2*(0,87 g+1))/ g2
2 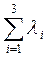
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (1 , 0 , 0 ,1 )= 0,9*10-2 +0,9*10-2*(0,87g+1)1/2
V (1 , 1 , 0 ,0 )
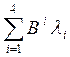 =
0,9*(1+2*10-3)*10-2+0,9*10-2=1,8*10-2+1,8*10-5;
=
0,9*(1+2*10-3)*10-2+0,9*10-2=1,8*10-2+1,8*10-5;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}= 4*
-(Bi)2]
}= 4* ![]() -
4*0,81 *10-8
-
4*0,81 *10-8
2 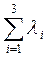
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (1 , 1, 0 ,0 )= 1,8*10-2+1,8*10-5+0,2*10-2 *(1-g*0,81*10-2 )1/2
V (1 , 0 , 1 ,0 )
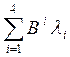 =
0,9*10-2;
=
0,9*10-2;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}= 7,13*10-6+ 4,0713*
-(Bi)2]
}= 7,13*10-6+ 4,0713*![]()
2 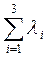
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V(1 , 0 , 1 ,0 )= 0,9*10-2 +0,1*10-2*(7,13g+4,0713 )1/2
V (1 , 0 , 1 ,1 )
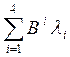 =
1,1*10-2;
=
1,1*10-2;
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=
-(Bi)2]
}=![]() (0,81+0,713*10-3)-
10-4 *(0,16*10-6)
(0,81+0,713*10-3)-
10-4 *(0,16*10-6)
2 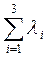
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V(1 , 0 , 1 ,1 )= 1,1*10-2+10-2*(0,8*10-3 - g*0,16*10-6)1/2
V (1 , 1 , 0 ,1 )
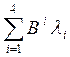 =
2*10-2+2,59*10-5+0,79*10-8
=
2*10-2+2,59*10-5+0,79*10-8
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=0,81*10-4 (-1,7*10-3 - 7,9*10-6-
4,21*10-9-0,7744*10-12)
-(Bi)2]
}=0,81*10-4 (-1,7*10-3 - 7,9*10-6-
4,21*10-9-0,7744*10-12)
2 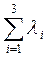
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (1 , 1 , 1 ,0 )= 2*10-2+2,59*10-5+0,79*10-8+10-2*0,9*
g (-1,7*10-3 - 7,9*10-6- 4,21*10-9-0,7744*10-12)1/2
V (1 , 1 , 1 ,0 )
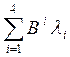 = 10-2*1,8*(1+10-3)
= 10-2*1,8*(1+10-3)
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=4*
-(Bi)2]
}=4*![]() +10-6(0,14
–0,39*10-4)
+10-6(0,14
–0,39*10-4)
2 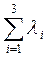
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (1 , 1 , 1 ,0 )= 1,8*10-2+10-3*(0,14g + 4)1/2
Расчет Dд соответствует задаче поиска max
V (1 , 1 , 1 ,1 )
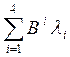 =
1,8*10-2+2*10-3 +2,6*10-5+0,8*10-8
=
1,8*10-2+2*10-3 +2,6*10-5+0,8*10-8
![]()
![]()
![]() +
+ ![]() [S
[S![]() -(Bi)2]
}=10-4 (0,1539 -0,44*10-3 -3,24*10-9- 1,8*10-6
-0,63*10-12)
-(Bi)2]
}=10-4 (0,1539 -0,44*10-3 -3,24*10-9- 1,8*10-6
-0,63*10-12)
2
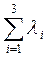
![]() Sj
Sj![]()
![]() j Cij
j Cij ![]() =0
=0
V (1 , 1 , 1 ,1 )= 2*10-2+2,6*10-5+0,8*10-8+g *10-2*(0,1539 -0,44*10-3- 1,8*10-6 -3,24*10-9 -0,63*10-12)1/2
Наибольшее значение функция V (α1 , α2 , α3 ,… α N ) принимает при комбинации
V (1 , 1 , 1 ,1 ), т.е. при α1 = α2 = α3 = α 4=1
Таким образом Dд = 10-2 * (2 + g * 0,4)
3.Экспериментальное определение МХ ИК ИИС (по протоколу измерений)
3.1. Измерение метрологических характеристик ИК ИИС состоит в проведении многократного измерения выходного сигнала в разных точках диапазона в условиях, максимально приближенных к реальным рабочим условиям эксплуатации ИИС.
На вход ИК подают последовательность значений сигнала в пяти контрольных точках шкалы от минимального значения до максимального и регистрируют значения выходных сигналов. В протоколе измерений №1 приведены данные 6-ти значений результата многократного измерения и допустимое отклонение функции преобразования Dдоп ИК от номинального значения функции преобразования в каждой из точек (таблица 3).
Проводим вычисления:
S – меры неопределенности показаний ИК;
uθ – меры неопределенности поправки к показаниям ИК;
u - меры неопределенности измеряемой величины.
|
Данные в контрольных точках |
Результаты измерений в контрольных точках уij |
|||||||
|
j |
xj |
Dдоп |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
0,02 |
0,00 |
0,03 |
0,02 |
0,02 |
0,00 |
0,01 |
|
2 |
20 |
0,01 |
20,00 |
19,97 |
19,96 |
19,98 |
20,00 |
19,99 |
|
3 |
40 |
0,02 |
39,99 |
39,96 |
39,97 |
40,00 |
40,02 |
39,99 |
|
4 |
60 |
0,02 |
60,02 |
60,05 |
60,01 |
60,00 |
60,01 |
60,00 |
|
5 |
80 |
0,03 |
80,00 |
79,99 |
79,98 |
79,97 |
79,98 |
79,96 |
Результаты измерений и расчетов заносим в таблицу 4.
По результатам расчетов строим график y = f(x) зависимости выходной величины от входной с учетом полученных значений uj. Меру неопределенности входного параметра считаем пренебрежимо малой.
3.2. В каждой контрольной точке шкалы определим средние арифметические значения результата измерений по формуле:
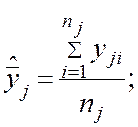 ( 26 )
( 26 )
где yji – результат измерения в j - ой контрольной точке, nj – число отсчетов в j - ой контрольной точке.
Используя значения таблицы 3, выполним расчеты по формуле (26):
Контрольная
точка 1 (x1=0):
![]() 0,08/6 = 0,013
0,08/6 = 0,013
Контрольная
точка 2 (x2=20):
![]() 119,9/6=19,983
119,9/6=19,983
Контрольная
точка 3 (x3=40):
![]() 239,93/6=39,988
239,93/6=39,988
Контрольная
точка 4 (x4=60):
![]() 360,09/6=60,015
360,09/6=60,015
Контрольная
точка 5 (x5=80):
![]() 479,88/6=79,98
479,88/6=79,98
В каждой контрольной точке вычислим стандартное отклонение (мера неопределенности, оцениваемая по типу А):
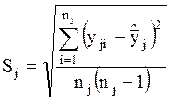 ( 27 )
( 27 )
Используя значения таблицы 3, выполним расчеты по формуле (27):
Контрольная
точка 1 (x1=0): 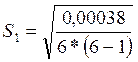 =(0,0000126)1/2=0,00355
=(0,0000126)1/2=0,00355
Контрольная
точка 2 (x2=20): 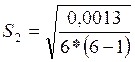 =(0,000044)1/2=0,00667
=(0,000044)1/2=0,00667
Контрольная
точка 3 (x3=40): 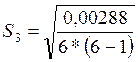 =(0,000076)1/2=0,00872
=(0,000076)1/2=0,00872
Контрольная
точка 4 (x4=60): 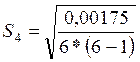 =(0,000058)1/2=0,00764
=(0,000058)1/2=0,00764
Контрольная
точка 5 (x5=80): 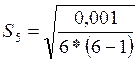 =(0,000033)1/2=0,00577
=(0,000033)1/2=0,00577
В каждой контрольной точке вычислим меру неопределенности поправки к показаниям ИК, вычисляемую по типу В. При этом в качестве математической модели неопределенной ситуации примем равномерный закон распределения вероятности:
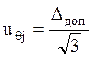 ( 28 )
( 28 )
Используя значения таблицы 3, выполним расчеты по формуле (28):
Контрольная
точка 1 (x1=0): 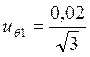 = 0,01154
= 0,01154
Контрольная
точка 2 (x2=20):
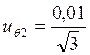 = 0,00577
= 0,00577
Контрольная
точка 3 (x3=40): 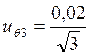 = 0,01154
= 0,01154
Контрольная
точка 4 (x4=60):
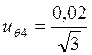 = 0,01154
= 0,01154
Контрольная
точка 5 (x5=80):
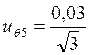 = 0,01731
= 0,01731
В каждой контрольной точке вычисляем меру неопределенности измеряемой величины.
![]() ( 29 )
( 29 )
Принимаем коэффициент охвата k=2.
Используя значения таблицы 4 и ранее полученные значения, выполним расчеты по формуле (29):
Контрольная точка 1 (x1=0): u1=2*(0,0000126+0,0001332)1/2=0,024
Контрольная точка 2 (x2=20): u2=2*(0,000044+0,000033)1/2=0,012
Контрольная точка 3 (x3=40): u3=2*(0,000076+0,0001332)1/2=0,029
Контрольная точка 4 (x4=60): u4=2*(0,000058+0,0001332)1/2=0,028
Контрольная точка 5 (x5=80): u5=2*(0,000033+0,0002996)1/2=0,036
|
Данные в контрольных точках |
Результаты измерений в контрольных точках уij |
Результаты расчетов |
|||||||||
|
j |
xj |
Dдоп |
1 |
2 |
3 |
4 |
5 |
6 |
Sj |
uθj |
uj |
|
1 |
0 |
0,02 |
0,00 |
0,03 |
0,02 |
0,02 |
0,00 |
0,01 |
0,00355 |
0,01154 |
0,024 |
|
2 |
20 |
0,01 |
20,00 |
19,97 |
19,96 |
19,98 |
20,00 |
19,99 |
0,00667 |
0,00577 |
0,012 |
|
3 |
40 |
0,02 |
39,99 |
39,96 |
39,97 |
40,00 |
40,02 |
39,99 |
0,00872 |
0,01154 |
0,029 |
|
4 |
60 |
0,02 |
60,02 |
60,05 |
60,01 |
60,00 |
60,01 |
60,00 |
0,00764 |
0,01154 |
0,028 |
|
5 |
80 |
0,03 |
80,00 |
79,99 |
79,98 |
79,97 |
79,98 |
79,96 |
0,00577 |
0,01731 |
0,036 |
3.3. По результатам расчетов построим график y = f(x) зависимости выходной величины от входной с учетом полученных значений uj. Меру неопределенности входного параметра считаем пренебрежимо малой.
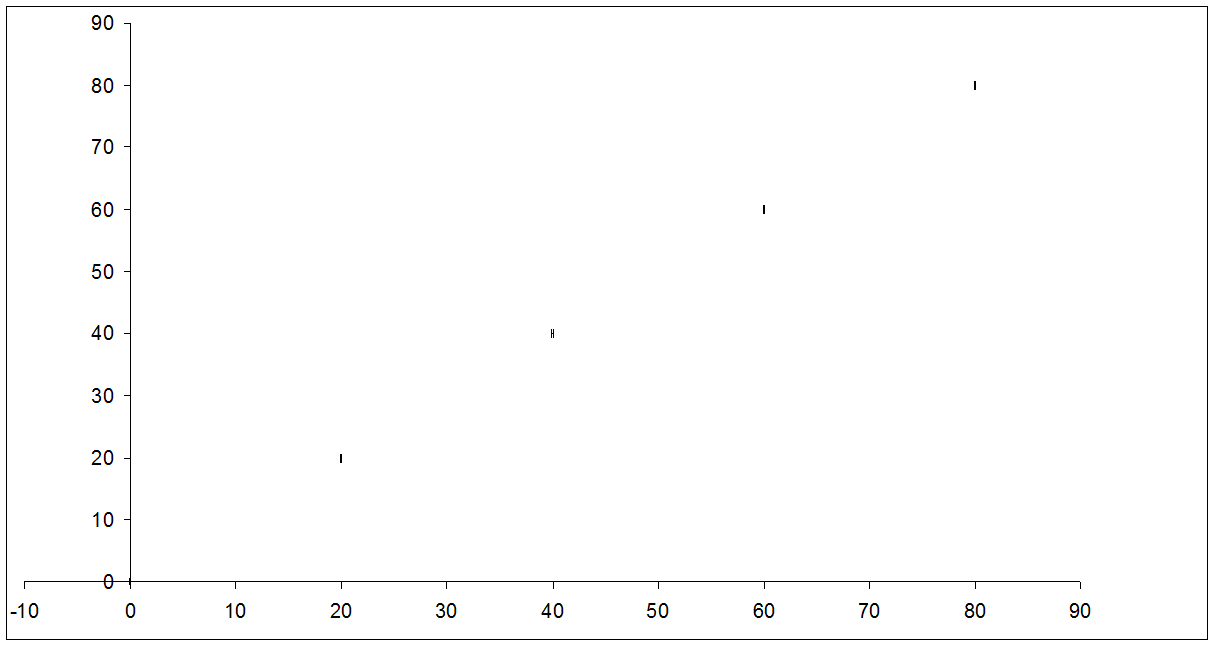
рис. График y = f(x)
4.1.Рассчитаем объем представительной выборки измерительных каналов, предназначенных для исследования каждого из параметров по формуле
![]()
![]()
![]()
![]()
![]()
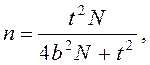 (
37 )
(
37 )
где
число ИК, составляющих генеральную совокупность:
ИК давления, уровняNд=40
ИК расходаNр=80
ИК температурыNт=360 допускаемое отклонение репрезентативности в процентах, определяемое по данным опытной эксплуатации ИК ИИС,b=10%, гарантируется с вероятностью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.