Создание нейронной сети со слоем Коханена

plot(start(1,1), start(2,1),'b+', record(1,:), record(2,:));  % Посторенниеграфика

xlabel('a(1)');

ylabel('a(2)');

title ('Результат работы сети Хопфилда')

Результат иллюстрируется рис.2.

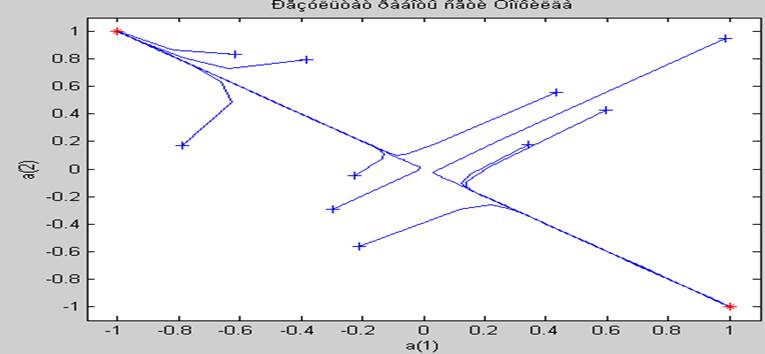
Рис. 2    Сеть Хопфилда после 10 выполнений программы

Министерство образования и науки РФ

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Комсомольский - на - Амуре государственный технический университет»

ИНИИТ (ИЭФ)

Кафедра информационных систем

ЛАБОРАТОРНАЯ РАБОТА

по дисциплине: Интеллектуальные информационные системы

вариант №1

Проверил преподаватель:

Амосов О.С.

Выполнил:

студент группы 3ПИ-3а-1

Кондакова Е.П.

2005

         Задание 1. Необходимо построить и обучить нейронную сеть для аппроксимации табличной функции , . Разработать программу, которая реализует нейросетевой алгоритм аппроксимации и выводит результаты аппроксимации в виде графиков.

         Решение

Для решения задачи воспользуемся пакетом Neural Networks Toolbox математической системы MatLAB (версии 5.2 или 6.1). Это инструментальное средство служит для проектирования, моделирования, обучения и использования множества известных архитектур НС, от базовых моделей персептронов до современных ассоциативных и самоорганизующихся сетей.

Для решения задачи воспользуемся функцией  – создания «классической» многослойной НС с обучением по методу обратного распространения ошибки.                                                                                                                             

Для выполнения задания 1 задана табличная функция в виде

                                                                                                                                Таблица 1

Процедура создания и использования данной НС описывается следующим образом.

 Программа

P = [0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2];                

% входные данные (аргумент)

T = [2.05 1.94 1.92 1.87 1.77 1.88 1.71 1.60 1.56 1.40 1.50 1.26 0.99 0.97 0.91 0.71 0.43 0.54 0.19 0.01 ];                                                                                                                                                                                                                         %входные данные (значение функции)

net = newff([0 2],[5 1],{'tansig' 'purelin'});                 % создание нейронной сети

net.trainParam.epochs = 100;                             % задание числа эпох обучения

net = train(net,P,T);                                                       % обучение сети

y = sim(net,P);                                                              % опрос обученной сети

figure (1);

hold on;

xlabel ('P');

ylabel ('T');

plot(P,T,P,y,'o'),grid;                                                      %;вывод  графиков

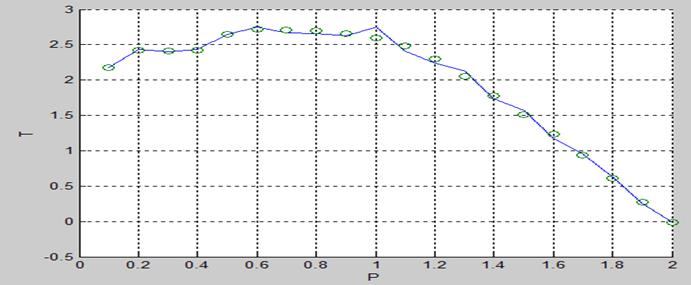
Рис.1 Результат работы нейронной сети

         Задание 2. Проиллюстрировать процедуру нечеткого логического вывода для системы, которая описывается нечеткими правилами.

База знаний	Алгоритм вывода
П1: если x есть А1 и если y В1, то z есть С1; П2: если x есть А2 и если y В2, то z есть С2; П3: если x есть А3 и если y В3, то z есть С3.	Mamdani

Алгоритм Mamdani.

1.  Введение нечеткости. Находятся степени истинности для предпосылок каждого из правил:

A1(x0), A2(x0), A3(x0)

B1(y0), B2(y0), B3(y0)

2.  Логический вывод. Находятся уровни «отсечения» для предпосылок каждого из правил (с использованием операции min);

α1 = A1(x0) ^ B1(y0)

α2 = A2(x0) ^ B2(y0)

α3 = A3(x0) ^ B3(y0)

где через «^» обозначена операция логического минимума (min).

Затем находятся «усечённые» функции принадлежности:

C’1(z) = (α1 ^ C1(z));

C’2(z) = (α2 ^ C2(z));

C’3(z) = (α3 ^ C3(z)).

3.  Композиция. Производится объединение найденных усеченных функций с использованием операции max, далее обозначаемой «v», что приводит к получению итогового нечеткого подмножества для переменной вывода z с функцией принадлежности:

µ∑(z) = C(z) = C’1(z) v C’2(z) v C’3(z) =(α1 ^ C1(z)) v (α2 ^ C2(z)) v (α3 ^ C3(z)).

4.  Приведение к четкости. Проводиться для нахождения z0.

z0 = α1z1+α2z2+α3z3

α1 + α2 + α3

z0 = (A1(x0) ^ B1(y0))z1 + (A2(x0) ^ B2(y0))z2 + (A3(x0) ^ B3(y0))z3

(A1(x0) ^ B1(y0)) + (A2(x0) ^ B2(y0)) + (A3(x0) ^ B3(y0)). 

Система будет иметь два входа (А и B), и один выход C. Для аппроксимации функции с одной переменной использую среду MatLab. Командой Fuzzy из режима командной строки запускаю интерфейсную программу Fuzzy Logic.

В появившемся окне существуют поля входной, выходной функции и редактора правил. Переименуем блоки input1 в x,  input2 в y, а output1 в z (рис.2).

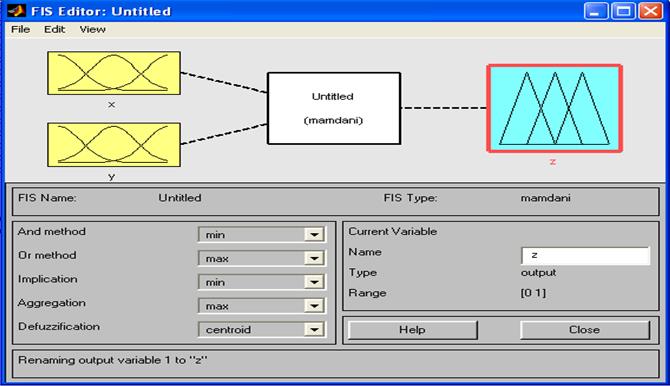
Рис.2 Окно редактора функции.

Щёлкнув по блоку x, открывается окно редактора функций принадлежности. Добавим функции принадлежности, для этого в меню Edit выберем опцию Add MFs (Рис.3). В появившемся диалоговом окне зададим тип (гауссовые) и количество функций принадлежности (3).

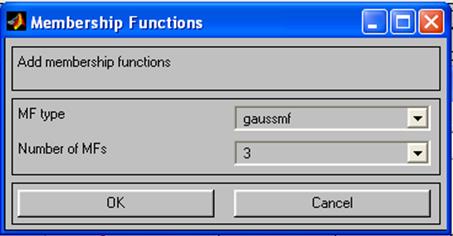
Рис.3 Диалоговое окно задания типа функции принадлежности

Затем в окне функций принадлежности в поле Range установим иапозон изменения значений x от 0 до 10. Для этого в поле Params (Параметры) задаём размах кривой и положение её центра.

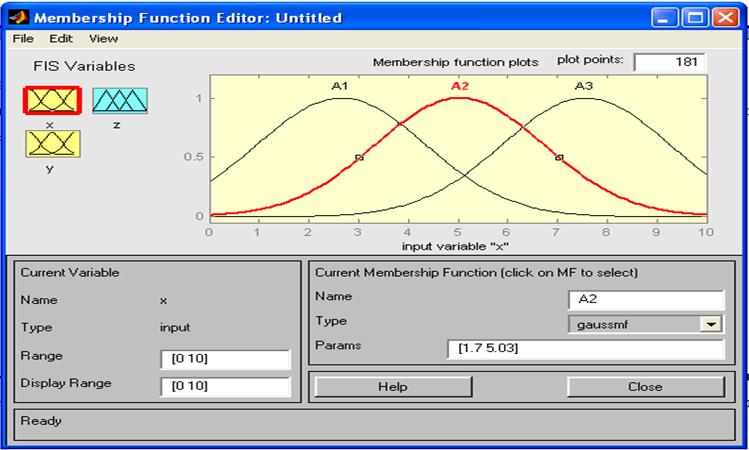
Рис.4 Окно редактора функции принадлежности.

Аналогично делаю для входной функции y.

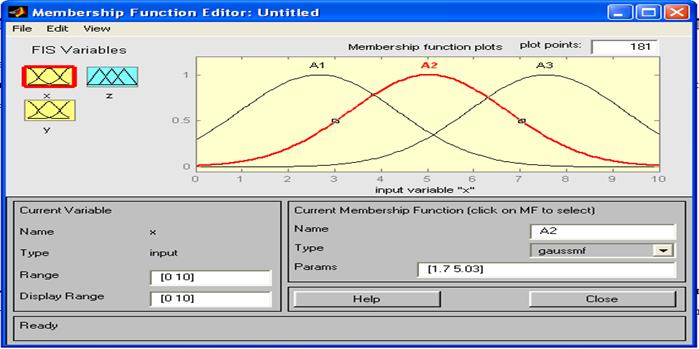
Рис.5 Окно редактора функции принадлежности

 

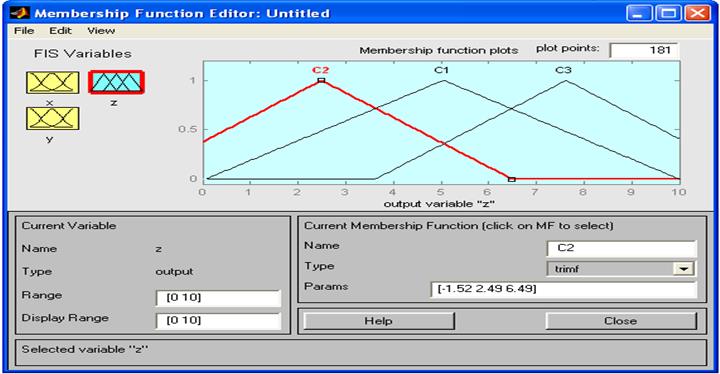
Рис.6 Окно редактора функции принадлежности

В окне FIS-редактора, щелкнув по среднему блоку, откроем окно редактора правил. При вводе каждого правила необходимо обозначить соответствие между каждой функцией принадлежности аргумента x и числовым значением y.

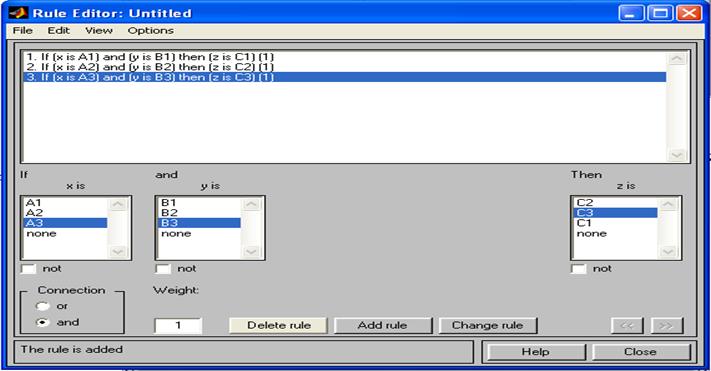
Рис. 7 Окно редактора правил

Существует возможность просмотра правил (Рис. 8). Для этого выберем позицию меню View – rules. В правой части (две колонки) окна в графической форме представлены функции принадлежности аргумента x, в левой – y с пояснением механизма