Непараметрические методы оценивания законов распределения случайной величины, страница 5

Выдвигаем гипотезу о законе распределения

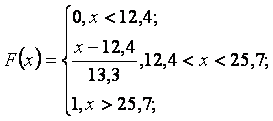
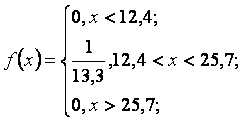
Проверка статистических гипотез распределения случайной величины

Критерий Пирсона.

         При использовании критерия Пирсона за меру несоответствия принимается величина , вычисленная по формуле:

        

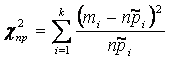
         где  - число интервалов

          - частота попадания в интервал

          - вероятность попадания случайной величины в интервал, вычисленная по проверяемому закону распределения.

         Вероятность попадания величины в заданный интервал при показательном распределении равна.

        

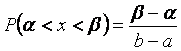
         Заполним таблицу с произведенными вычислениями по каждому интервалу

Номер интервала	1	2	3	4	5	6	7	8
Границы интервала	(12,4; 14,06)	(14,06; 15,72)	(15,72; 17,39)	(17,39; 19,05)	(19,05 ;20,71)	(20,71; 22,37)	(22,37; 24,04)	(24,04; 25,7)
Частота попадания	12	12	9	9	15	14	13	16
Вероятность попадания	0.125	0.125	0.125	0.125	0.125	0.125	0.125	0.125
	0.5	0.02	0.98	0.98	0.5	0.18	0.02	0.98