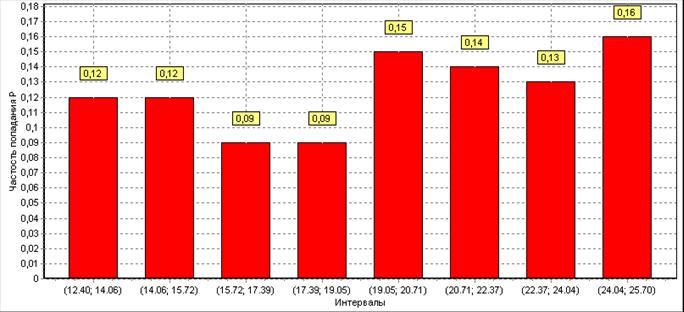
По данным полученного вариационного ряда построим гистограмму
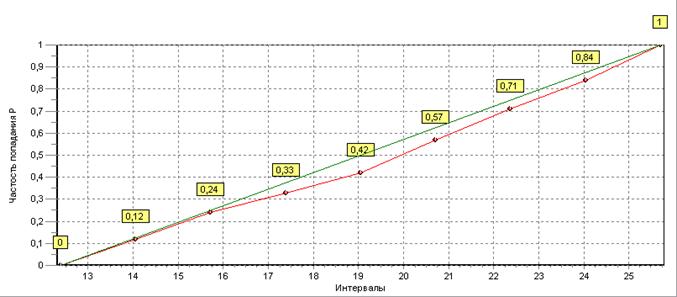 И график эмпирической функции распределения
И график эмпирической функции распределения
Проанализировав внешний вид графика функции распределения, можно выдвинуть гипотезу о том, что здесь представлен равномерный закон распределения случайной величины.
Параметрическое оценивание
Проведём
оценку параметров для показательного распределения, гипотезу о котором мы
выдвинули на предыдущем этапе. По условию доверительная вероятность ![]() , уровень значимости
, уровень значимости ![]()
Выполним оценку математического ожидания случайной величины по среднему арифметическому элементов выборки:
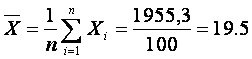
Для дисперсии исправленная выборочная дисперсия:
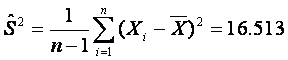
Точечными оценками параметров a и b берем величины:
a*=Xmin= 12,4; b*=Xmax= 25,7;
Доверительный интервал для математического ожидания:
![]() ,
n=100, β=0,95, α=1-0,95=0,05;
,
n=100, β=0,95, α=1-0,95=0,05;
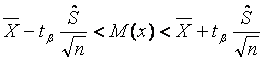 ;
;
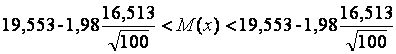 ;
;
![]() ;
;
![]() ;
;
Доверительный интервал для дисперсии:
Для вычисления нам необходимы
значения критериев распределения ![]() Пирсона, которые составляют
Пирсона, которые составляют ![]() и
и ![]() при уровне значимости
при уровне значимости ![]() и
и
![]() .
.
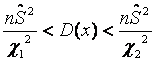
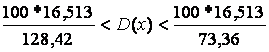
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.