Для построения интервального вариационного ряда необходимо найти распределение случайной величины по интервалам. Выполним расчет по определению ширины интервалов.
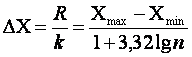
где 
-число интервалов
-минимальный
элемент выборки
-максимальный
элемент выборки
-размах выборки
Xmax= 25,7; Xmin= 12,4;
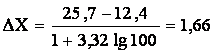
Берем количество интервалов равным 8.
Теперь необходимо найти частость попадания в интервал P*i, представителя интервала ãi и плотность относительной величины для каждого инетервала соответственно по формулам:
; ãi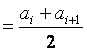
; 
;
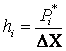Интервальный вариационный ряд:
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Границы интервала (a) |
(12,4; 14,06) |
(14,06; 15,72) |
(15,72; 17,39) |
(17,39; 19,05) |
(19,05 ;20,71) |
(20,71; 22,37) |
(22,37; 24,04) |
(24,04; 25,7) |
|
Частота попадания (n) |
12 |
12 |
9 |
9 |
15 |
14 |
13 |
16 |
|
Частость попадания (p) |
0,12 |
0,12 |
0,09 |
0,09 |
0,15 |
0,14 |
0,13 |
0,16 |
|
Представитель интервала (a*) |
13,23 |
14,89 |
16,55 |
18,22 |
19,88 |
21,54 |
23,2 |
24,87 |
|
Плотность попадания (h) |
0,07 |
0,07 |
0,05 |
0,05 |
0,09 |
0,08 |
0,08 |
0,1 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.