Обнаружение дефектов реализованными алгоритмами, страница 2

Оценка вероятности ложного обнаружения определяется по формуле:

,  ,

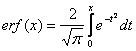где  - нижний и верхний пороги срабатывания.

В данном случае используем симметричные пороги  

При диагностировании изменения математического ожидания случайного процесса от

 до  и симметричных порогах  оценка среднего времени обнаружения определяется по формуле:

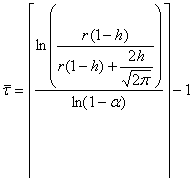,   где ,

 - округление сверху – ближайшее целое большее ,

 - дисперсия случайного процесса.

Алгоритм Пейджа

Решающая функция определяется как:

,

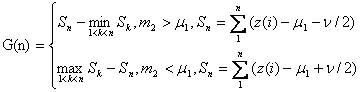где ,

- математическое ожидание выходного сигнала до появления дефекта,

- порог чувствительности.

Решение о наличии или отсутствии дефекта в каждый момент времени принимается на основе результатов сравнения:

 => дефекта нет,

=> есть дефект,

где  - порог срабатывания.

Модификация алгоритма (реккурентный вид)

Исходная формула для случая  преобразуется к виду:

, где , .

Начальные условия: .

Для случая  преобразуется к виду:

, где , .

Начальные условия: .

Теория АЭС

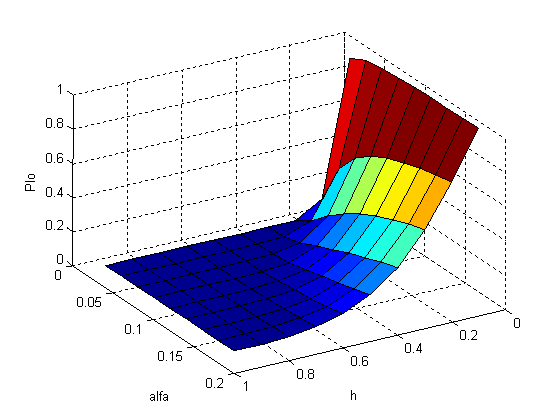
Рис. 2.1.1. Зависимость вероятности ложного обнаружения от параметров.

Из графика и данных таблицы видно, что с увеличением параметра alfa вероятность ложного обнаружения дефектов растет. С увеличением порога h вероятность P_lo падает.

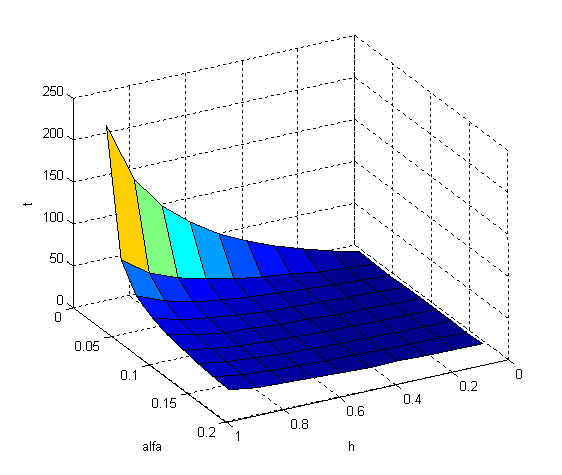
Рис. 2.1.2. Зависимость среднего времени обнаружения от параметров (r = 1).

Из графика и данных таблицы видно, что с увеличением параметра alfa среднее время обнаружения дефектов уменьшается. С увеличением порога h время t_обн увеличивается.

Аналитически рассчитанные пороги h:

	0,01	0,02
0,1	0,543	0,4905
0,15	0,674	0,609