Основы вычислительных конвейеров, страница 5

Конвейерный умножитель

Базовая ступень сумматора может также использоваться при построении различных конвейерных устройств целочисленного умножения. На рис. 2.27 показан умножитель типа 4х4 разряда, основанный на классическом получении частичных произведений по одному разряду за один раз, за которым следует серия конвейерных сумматоров с последовательным переносом, суммирующих эти члены. Расширенные варианты приведенной схемы могут с помощью этого же метода вычислять любые произведение вида NxN разрядов со скоростью одно произведение за один период синхронизации (независимо от N), но опять-таки за счет резкого увеличения числа схем задержки, необходимых для выравнивания и запоминания промежуточных результатов. Для сравнения отметим, что наилучшее время, за которое неконвейерный умножитель способен вычислить результаты, пропорционально lgN в степени 2.

Оба эти конвейера узко однофункциональны. А как сделать хотя бы простой многофункциональный конвейер?

Для этого необходимо построить многофункциональную вычислительную ячейку и универсальную ячейку управления. Например, такие:

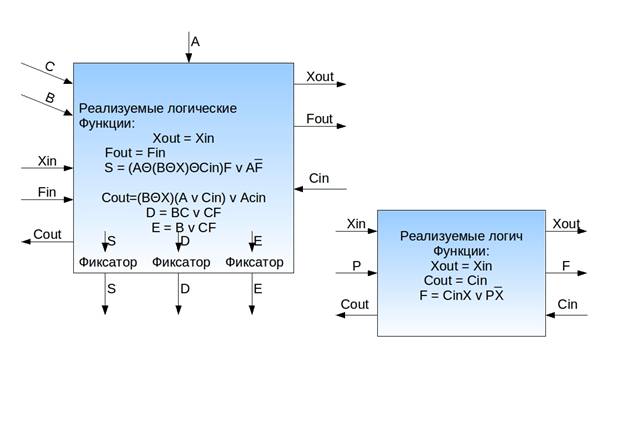
Управляющий вход Х задает: должно ли значение на входе В быть неизменным или заменяться на дополнение.  на управляющем входе F задает передачу значения с А на выход S, а 1 задает сложение значения на входе А со значениями на выходе В и т.д.

На таких ячейках уже можно построить многофункциональный конвейер. При этом выбором входных сигналов и подмножеств множества выходов определяется реализуемая операция.

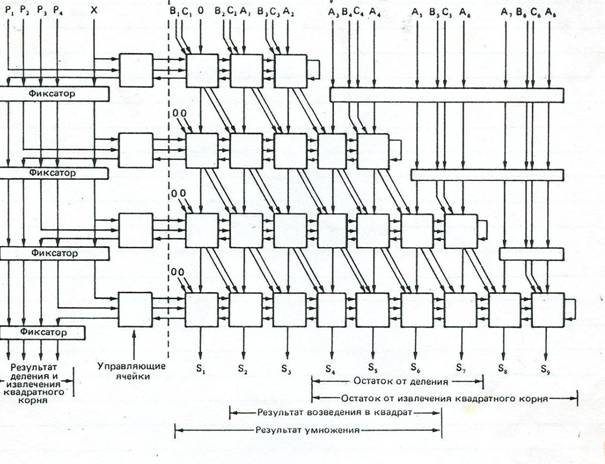
На рисунке выше показан пример комбинации ячеек, чтобы выполнять умножение, деление, возведение в квадрат и извлечение квадратного корня:

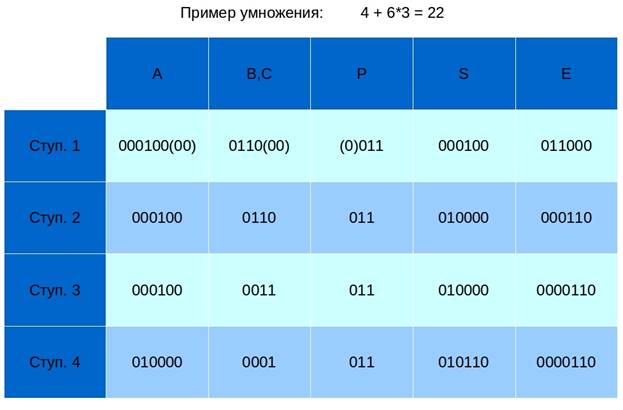
Результат: S1S2…S6 = 0101102 = 2210

Дальнейшим развитием многофункционального конвейера будет конвейер с множественными путями (ветвящийся). Это отказ от линейности! А значит, все усложняется. Но приведем относительно легкий пример: конвейер для умножения чисел с плавающей запятой. Напомним три подфункции: умножение мантисс, сложение порядков и нормализация. Сложение чисел с плавающей запятой тоже разделяется на три подфункции: начальное выравнивание, сложение мантисс и нормализация результата.

Очевидно, что фиксированная запятая составит к вышеупомянутым примерам частный случай.

Все можно реализовать примерно на такой структуре:

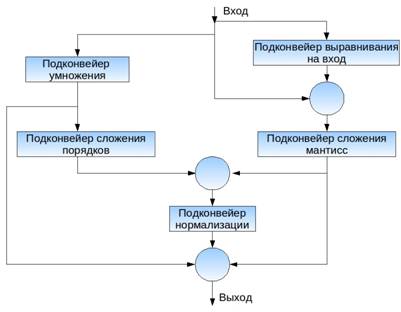
Использование конвейеров:

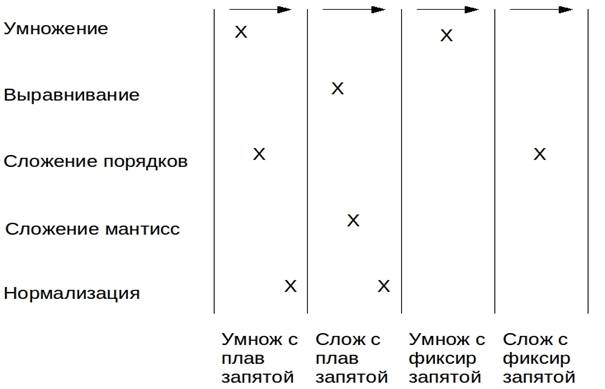
Обобщенно показан многофункциональный конвейер со многими путями, единый на 4 операции. Управляющее устройство обеспечивает ввод информации о требуемом маршруте в конвейере при каждой инициации операций. Но в полном соответствии с теорией возникают структурные помехи (столкновения) между различными инициациями.

Например, пусть за операцией сложения чисел с ПЗ через короткое время пойдет операция сложения чисел с ФЗ. Если не предусмотреть специально взаимную синхронизацию, то подконвейер сложения мантисс две операции попытаются использовать одновременно.

Следующий шаг в развитии конвейеров – конвейеры с обратной связью. А они могут применяться для обработки рекурсий (рекуррентных выражений). Сюда может быть отнесено много задач обработки сигналов с обобщенной формулой:

x (i) = f (a (i), x (i-1), …, x (i-m)), где, например,

a (i) – i-й раз измеренное значение входного сигнала;

x (i) – соответствующее значение результата вычислений.

Прямая реализация на конвейере возможна:

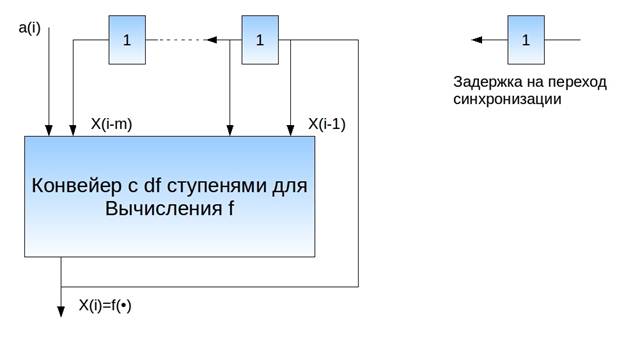
Однако такая реализация резко снижает производительность: если число ступеней для вычисления f равно d, то время от начала вычисления x(i) до завершения составит d периодов синхронизации; а поскольку x(i+1) зависит от x(i), то до завершения вычисления x(i) нельзя начать вычисления x(i+1). Вся конвейерность полетела к черту!