Моделирование объектов систем компьютерного управления на базе платы сопряжения L-154

Теоретическая часть.

                В основе моделирования на АВК систем второго порядка лежит теория подобия: похожие физические процессы описываются одинаковыми уравнениями. Точность моделирования определяется степенью подобия. Использование для моделирования АВМ имеет ряд преимуществ: высокое быстродействие, наблюдение в темпе процесса любого числа составляющих в соответствующем масштабе времени. Основным решающим элементом в АВК является операционный усилитель. На первом этапе моделирования составляется схема набора. На втором этапе решается задача количественного подобия, т.е. устанавливаются зависимости между исходными и машинными переменными.

Схема эксперимента.

Рассматривается моделирование объекта, заданного линейным дифференциальным уравнением второго порядка.

Рассмотрим случай, когда

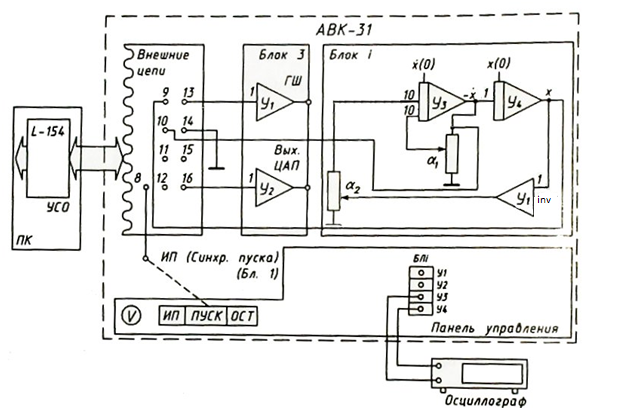
Рис. Схема набора.

1.  A1 = 0

Так как отсутсвует коэффициент a1, в системе будут незатухающие автоколебания. Частота автоколебаний находится как . Соответсвенно период с.

Смоделируем эту систему в matlab.

Схема моделирования показана на рисунке.

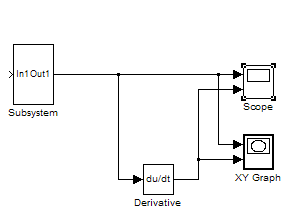
В результате получили следующее:

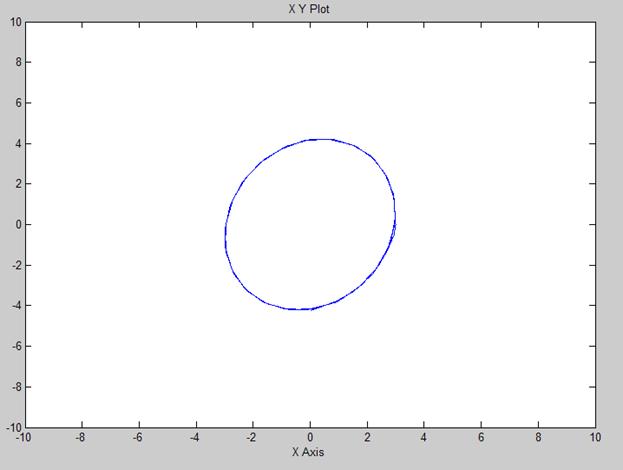
Рис. Фазовый портрет

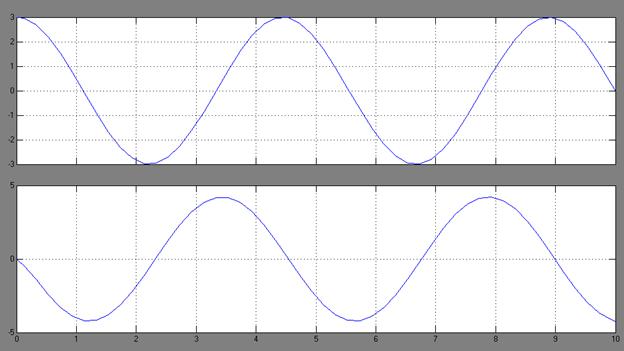
Рис. и

2.  Найдём коэффициент а1, при котором система находится в точке бифуркации.

В matlab соответственно получаем следующее:

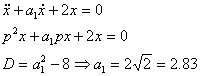
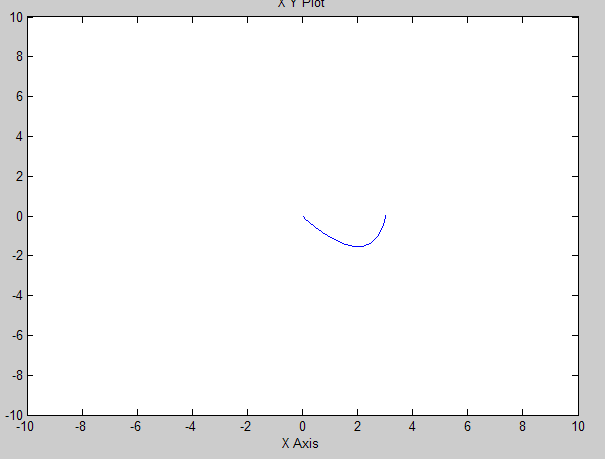
Рис. Фазовый портрет

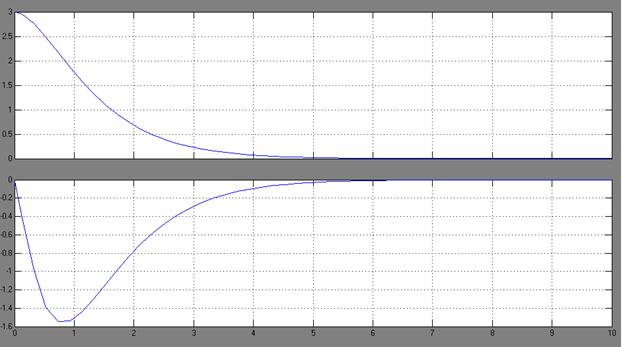
Рис. и

3.  Аналогичные графики построим для коэффициента  и .