Исследование особенностей квантования сигналов в WDV и анализ источников погрешностей измерений, страница 3

Рис.5. Зависимость максимальной ошибки e от периода дискретизации Т₀

1к – 1 Тц; 2к – 2 Тц; 3к – 5 Тц; 4к – 10 Тц; Тц = 100 мс

Тк = Тс/2 – период квантования по т.Котельникова

Рис.6. Синусоидальный сигнал при различных периодах квантования (н.у. = 2)

Зависимость максимальной ошибки e от периода дискретизации Т₀.

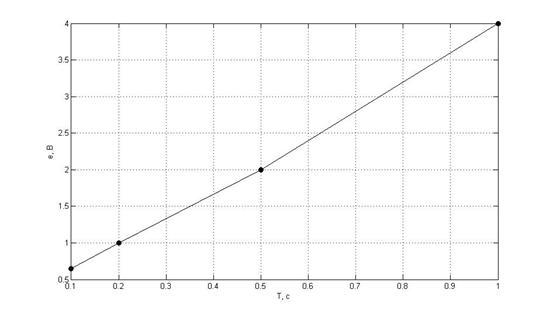
Рис.7. Зависимость максимальной ошибки e от периода дискретизации Т₀

2)  Фазовые искажения полезного сигнала при: φ = f(T₀), T₀ = var

C увеличением периода квантования помимо амплитудных искажений возникают фазовые искажения. Это связано с тем, что интерполяция функции производится посередине локального линейного участка. То есть присутствует задержка в реакции дискретной системы по сравнению с непрерывной. Эта задержка (фазовый сдвиг) равна половине ½ Тк. По  т.Котельникова наибольший допустимый период составляет 1с, то сдвиг по фазе равен 0,5с или 90 градусов.

Зависимость фазового сдвига φ от периода дискретизации Т₀.

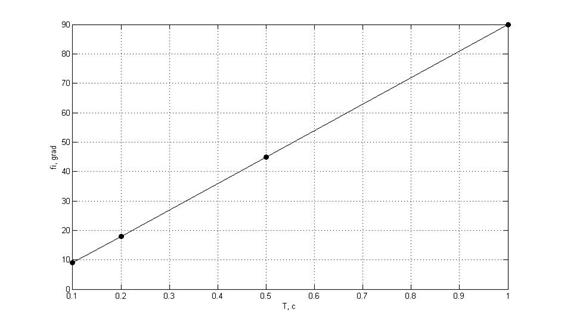
Рис.8. Зависимость фазового сдвига φ от периода дискретизации Т₀

3)  Определение погрешности фиксатора “0”-го порядка (e₀) для минимально возможной дискретизации.

В п.1) показано, что с уменьшением периода квантования уменьшается и погрешность квантования по амплитуде. Определим наименьшее возможное в данной системе значение такой ошибки.

Ошибка возрастает вместе с модулем производной оцифровываемого сигнала. Для синуса наибольшее значение его достигается в окрестностях нуля функции. Соответственно максимальное значение ошибки будет равно кванту величины сигнала на этом участке. Опытным путем установлено, что погрешность равна 0,023 В.