Информатика и выч. техника \ Алгоритмизация задач управления

Исследование особенностей квантования сигналов в WDV и анализ источников погрешностей измерений, страница 2

        Представим модель сигнала в виде   где  - помеха в виде моночастотного сигнала с амплитудой  и частотой .

      Так как мы можем варьировать частоту квантования , то можем производить опрос датчиков как в условиях формального выполнения теоремы Шеннона-Котельникова, так и при нарушении этих условий.  В этом случае транспонированный квантованием сигнал будет зависеть от  соотношения  и .

3.  Результаты экспериментов

3.1.Определение погрешности квантования по уровню постоянного входного сигнала без шума и с шумом измерения (схема эксперимента рис.2.)

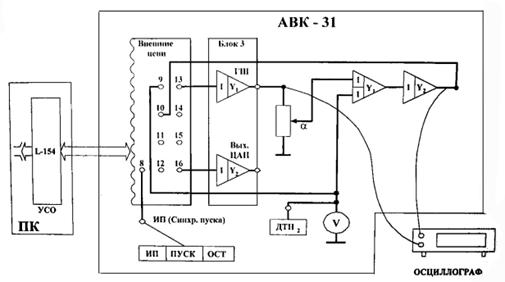
Рис.2. Схема лабораторной установки

Цена младшего разряда составляет 0,0025 В.

Канал 9 (сигнал в отсутствие шума)

Канал 10 (сигнал с наличием шума)

-∆max

+∆max

-∆max

+∆max

-0.0025

0.0075

-0.8300

0.8750

1 мл.разряд

3 мл.разряда

332

350

В отсутствие помех максимальная погрешность квантования сигнала составляет порядка единиц младшего разряда АЦП. В случае квантования сигнала с шумом эта погрешность возрастает на 2 порядка.

3.2.Исследование квантования непрерывного сигнала (схема эксперимента рис.3.)

fc = 0.5 Гц, Tc = 2c

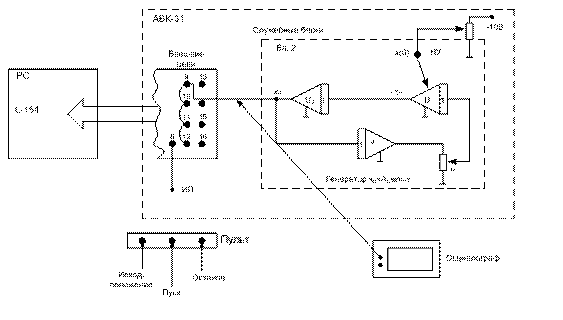
Рис.3. Схема лабораторной установки


1)  Исследование влияния дискретизации на погрешность измерения синусоидального сигнала вплоть до потери сигнала (н.у. нулевые).

1.jpg

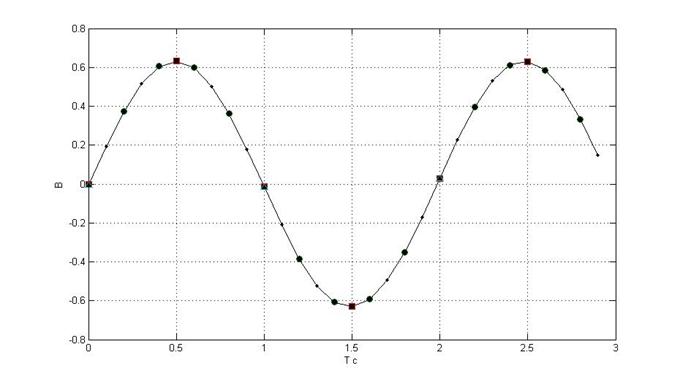
1к – 1 Тц; 2к – 2 Тц; 3к – 5 Тц; 4к – 10 Тц; Тц = 100 мс

Тк = Тс/2 – период квантования по т.Котельникова

Рис.4. Синусоидальный сигнал при различных периодах квантования (н.у. = 0)

Зависимость максимальной ошибки e от периода дискретизации Т0.

Т0, с

e, В

0,1

0,19

0,2

0,39

0,5

0,63

1

0,01
Скачать файл