Содержание
Описание работы регулятора. 3
Функциональная схема регулятора. 4
Структурная схема регулятора. 4
Уравнение динамики объекта регулирования. 4
Динамика датчика скорости. 5
Динамика сервомеханизма. 6
Уравнение динамики САР. 7
Определение условий устойчивости. 9
Выбор способа решения дифференциального уравнения движения САР. 13
Решение дифференциального уравнения свободного движения САР. 13
ИЗОДРОМНЫЙ РЕГУЛЯТОР С СИЛОВОЙ ОБРАТНОЙ ОТРИЦАТЕЛЬНОЙ ГИДРАВЛИЧЕСКОЙ СВЯЗЬЮ
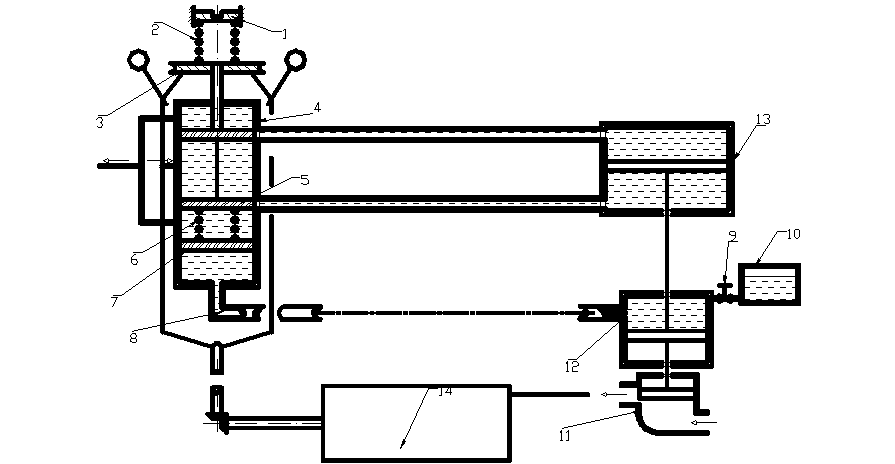
Конструктивная схема САР скорости вращения паровой турбины
1. – верхняя подвижная опора пружины регулятора, 2. – настроечная пружина регулятора, 3. – муфта датчика скорости, жестко связанная с золотником усилителя. 4. – втулка гидроусилителя, 5 – золотник гидроусилителя, 6. – пружина изодрома, 7. – местная обратная отрицательная гидравлическая гибкая силовая связь, 9. – игольчатый клапан изодрома, 10. – масляная ванна, 11. – паровой клапан, 12. – дающий поршень изодрома, 13. – двуполостной поршневой исполнительный механизм, 14. – объект регулирования (паровая турбина) .
Система находится в равновесии, т.е. нагрузка постоянна, подача пара на турбину пропорциональна нагрузке, центробежная сила грузов приведенная к оси вращения равна усилию предварительного затяга пружины, окна золотника перекрыты, поршень исполнительного механизма и следовательно клапан находятся в каком-то положении и неподвижны.
Статический этап работы регулятора
Нагрузка на турбину изменилась, например, уменьшилась, тогда обороты турбины начинают возрастать, грузы датчика скорости расходятся, и муфта датчика идет вверх и тащит за собой золотник усилителя. Масло из напорной магистрали поступает, через окна усилителя в верхнюю полость исполнительного механизма, а нижняя полость соединяется со сливной магистралью. Поршень исполнительного механизма под действием перепада давления идет вниз, перемещая паровой клапан на уменьшение подачи пара в турбину. Одновременно вниз движется дающий поршень изодрома, что приводит к разряжению в гидросвязи. Приемный поршень изодрома движется вниз и через пружину изодрома тащит вниз золотник усилителя и связанную с ним муфту датчика. После нескольких колебаний, наступает первое равновесное состояние, при котором муфта датчика и золотник усилителя занимают прежнее положение, при новом положении поршня исполнительного механизма и новой подаче пара.
Астатический этап работы регулятора
Постепенно масло из масляной ванны просачивается, через игольчатый клапан изодрома в гидросвязь, разряжение в которой начинает уменьшаться. Усилие пружины изодрома постепенно ослабевает, окна гидроусилителя приоткрываются, и вышеописанный процесс повторяется в уменьшенном масштабе. В конце концов, разряжение в гидросвязи полностью снимается. Связь между дающим и приемным поршнями изодрома обрывается, а следовательно обрывается и МООС и регулятор превращается в астатический.
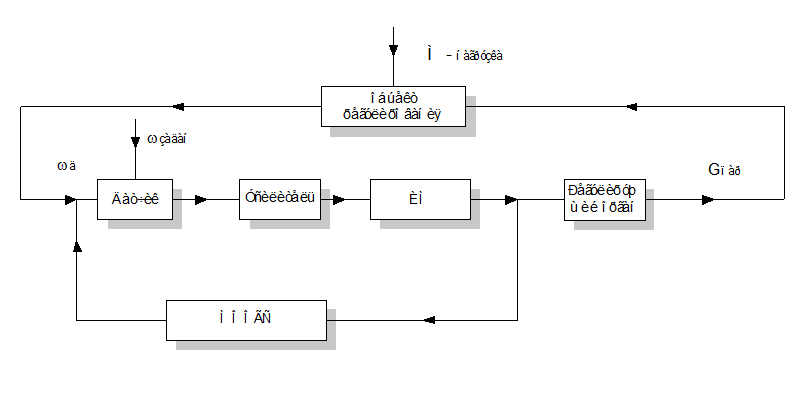
Функциональная схема регулятора САР скорости вращения паровой турбины
САР представлена четырьмя типовыми динамическими звеньями:
Объект регулирования – апериодическое звено 1 порядка,
Датчик скорости – апериодическое звено 1 порядка,
Сервомеханизм – интегрирующее звено,
МООС – дифференцирующее звено.
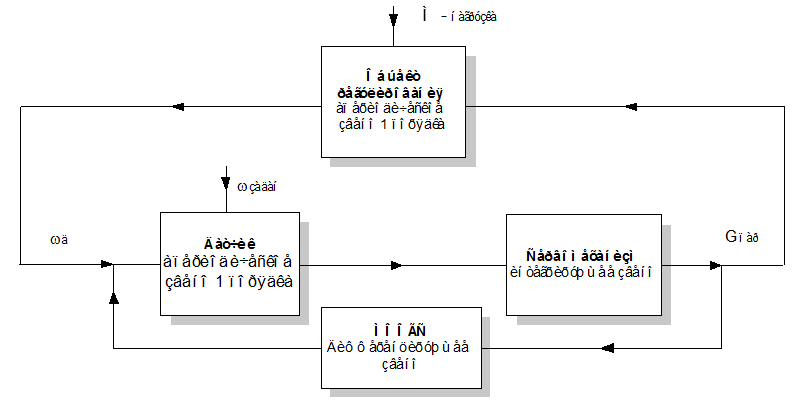
Структурная схема регулятора САР скорости вращения паровой турбины
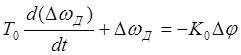 ,
,
где ![]() ,
, ![]() - постоянная времени объекта
регулирования;
- постоянная времени объекта
регулирования;
![]() ,
, ![]() - приращение частоты вращения турбины;
- приращение частоты вращения турбины;
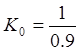 , или
, или ![]() - статический передаточный коэффициент
усиления объекта регулирования;
- статический передаточный коэффициент
усиления объекта регулирования; ![]() ,
, ![]() - перемещение штока парового клапана.
- перемещение штока парового клапана.
Угловая скорость:
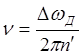 , где
, где ![]() ,
, ![]() -
номинальная частота вращения турбины,
-
номинальная частота вращения турбины,
следовательно
![]() .
.
Ход штока парового клапана:
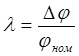 ,
, ![]() , [мм], тогда
, [мм], тогда
![]() .
.
Исходное уравнение примет вид
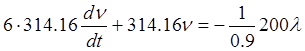 ,
,
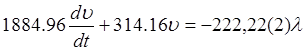 ,
,
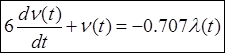 .
.
Преобразованное по Лапласу уравнение имеет вид
![]() ,
,
Передаточная функция есть отношение преобразованной по Лапласу выходной координаты к преобразованной по Лапласу входной координате.
Следовательно: передаточная функция объекта регулирования
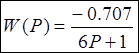 .
.
В общем случае динамика центробежного датчика скорости описывается апериодическим звеном второго порядка, но с целью понижения порядка дифференциального уравнения свободного движения САР, с достаточной точностью можно описать датчик, апериодическим звеном первого порядка [1].
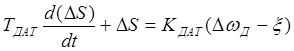 ,
,
где
![]() ,
, ![]() - постоянная времени датчика;
- постоянная времени датчика;
![]() ,
, ![]() - приращение хода муфты датчика;
- приращение хода муфты датчика;
![]() -
статический передаточный коэффициент усиления датчика;
-
статический передаточный коэффициент усиления датчика;
![]() ,
, ![]() - приращение частоты вращения турбины;
- приращение частоты вращения турбины;
![]() ,
, ![]() - приращение выходной координаты МООС.
- приращение выходной координаты МООС.
Приращение хода муфты датчика:
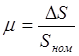 ,
, ![]() ,
, ![]() ;
;
следовательно,
![]() .
.
Приращение выходной координаты МООС:
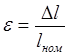 , где
, где ![]() ,
, ![]() ,
,
тогда, ![]() .
.
Как было показано выше,
![]() .
.
Тогда исходное уравнение примет вид
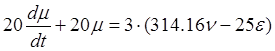 ,
,
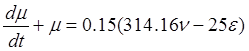 ,
,
Уравнение динамики датчика в безразмерных координатах
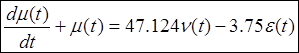
После преобразования по Лапласу уравнение
![]()
Передаточная функция датчика имеет вид
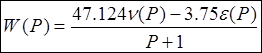 .
.
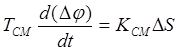 ,
,
![]() ,
, ![]() - постоянная времени сервомеханизма;
- постоянная времени сервомеханизма;
![]() ,
, ![]() - приращение хода муфты сервомеханизма;
- приращение хода муфты сервомеханизма;
![]() -
статический передаточный коэффициент усиления сервомеханизма;
-
статический передаточный коэффициент усиления сервомеханизма;
![]() ,
, ![]() - перемещение штока парового клапана.
- перемещение штока парового клапана.
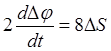 ,
,
Как было показано ранее
![]() ,
, ![]() .
.
После подстановки безразмерных координат в уравнение динамики сервомеханизма получим:
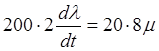 ,
,
или,
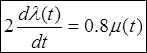
После преобразования Лапласа
![]() .
.
Передаточная функция сервомеханизма
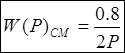 .
.
Динамика МООС
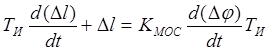 .
.
В безразмерных координатах
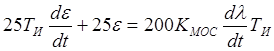 ,
,
или,
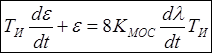 .
.
После преобразования Лапласа
![]()
Передаточная функция МООС
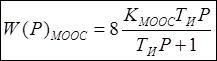 .
.
Таким образом:
|
Звено |
Уравнение динамики звена |
Передаточная функция звена |
|
Объект регулирования |
|
|
|
|
||
|
Датчик |
|
|
|
|
||
|
Сервомеханизм |
|
|
|
|
||
|
МООС |
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.