Изодромный регулятор с силовой обратной отрицательной гидравлической связью, страница 2

Уравнение динамики САР

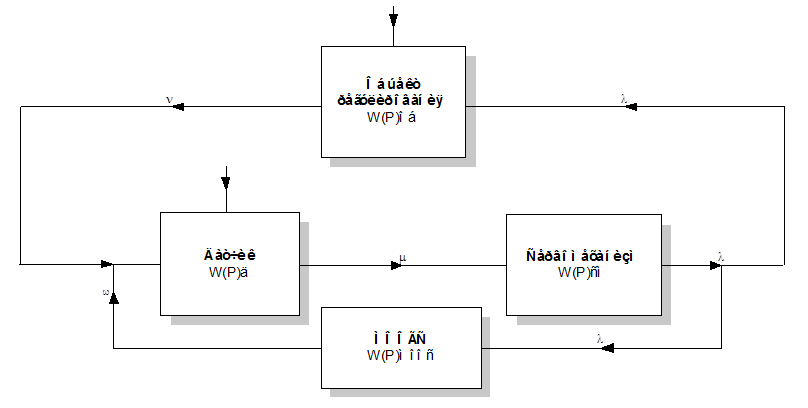
Определение искомого уравнения, через уравнения динамики элементов САР

Полученные уравнения динамики звеньев образуют систему уравнений, решая которую можно получить уравнение свободного движения системы.

Исходная система уравнений:

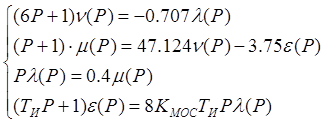
Решение системы уравнений:

,

,

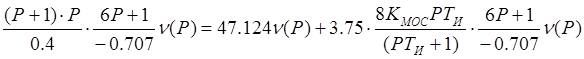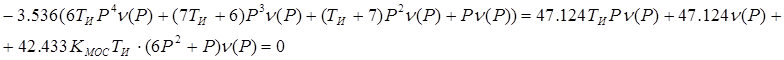
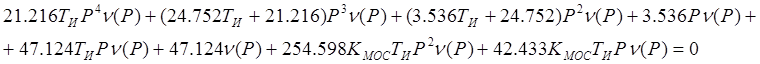
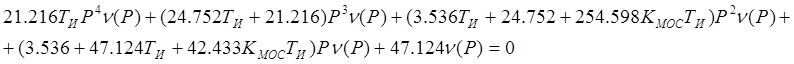
Уравнение свободного движения системы

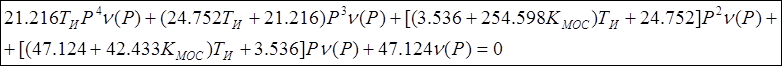
или в дифференциальной форме

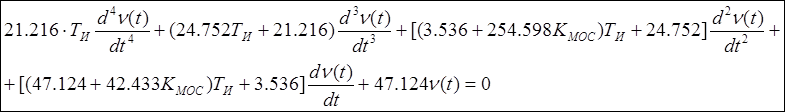
Определение искомого уравнения по общему уравнению свободного движения, через передаточные функции звеньев

,

,

, ,

,

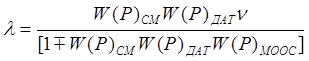, следовательно

,

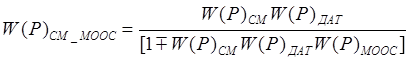для нашего случая

,

.

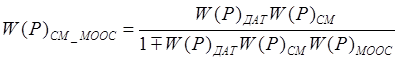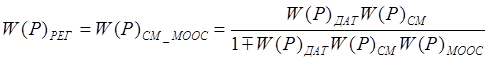Таким образом, передаточная функция САР:

,

,

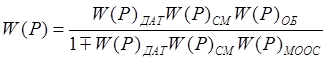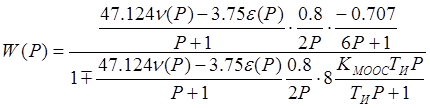Т.к. , то получим:

.

Определение условий устойчивости

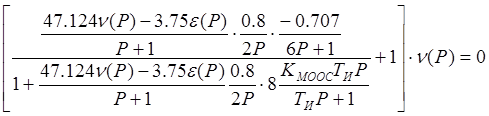Для определения условий устойчивости САР можно использовать критерии устойчивости Гурвица.

По первому условию Гурвица все коэффициенты характеристического уравнения должны быть положительны.

Дифференциальное уравнение

Характеристическое уравнение имеет вид

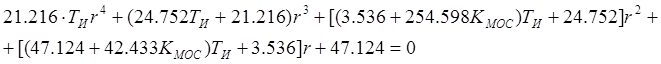
или,

,

где

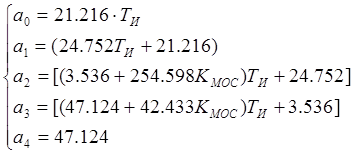
Т.к.  и , то первое условие Гурвица выполняется.

По второму условию Гурвица все определители, составленные из коэффициентов характеристического уравнения, положительны, в случае устойчивой системы.

,

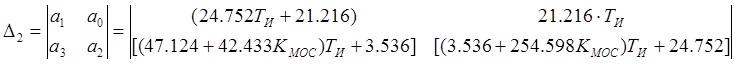
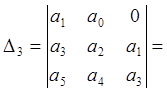
Решим данные определители как систему неравенств:

,

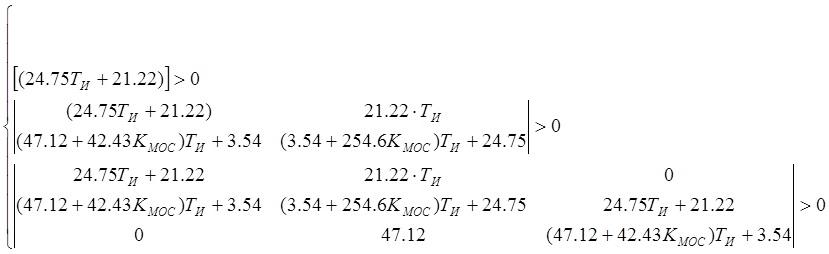
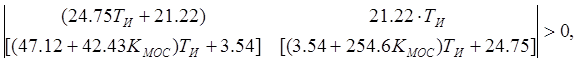
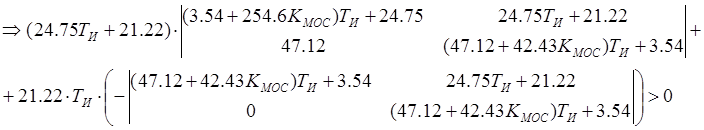
Таким образом:

1) 

2) 

3) 

Из первого неравенства следует,

, т.е.

Из второго неравенства выразим ,

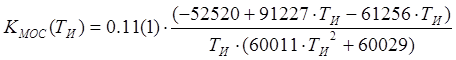
Из третьего,

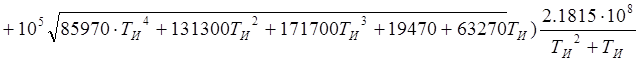
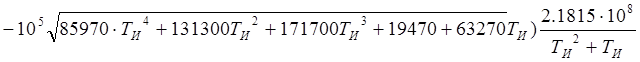
Определим на графике область, в которой выполняется вышеуказанные неравенства.

знаком «+» отмечены области, где выполняются все три неравенства.

Таким образом, решение  системы неравенств

,

,

,

.

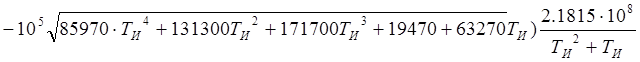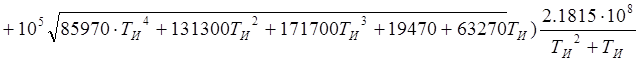Поскольку  и , то нас интересует только первый квадрант.

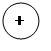
Знаком «+» обозначена область устойчивости САР

Для нашего случая, область устойчивости САР определяется следующими условиями:

,

.

Выбор способа решения дифференциального уравнения движения САР

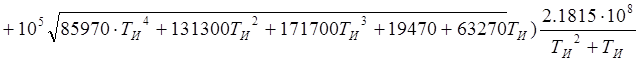Фундаментальные системы решений линейных однородных уравнений удается найти лишь для некоторых простейших типов таких уравнений. Одним из этих типов являются линейные однородные дифференциальные уравнения с постоянными коэффициентами. Интегрирование линейных однородных дифференциальных уравнений с постоянными коэффициентами в элементарных функциях сводится к чисто алгебраическим операциям [2].

Для каждого простого и кратного корня характеристического уравнения, можно составить систему из n различных решений дифференциального уравнения. Полученная система решений будет фундаментальной на интервале . Линейная комбинация этих решений с произвольными коэффициентами дает общее решение уравнения во всей плоскости  [2].

При решении характеристического уравнения возможны следующие корни:

Для случая простого действительного корня , частное решение есть ;

для случая - кратного действительного корня,  частных решений: , , …,;

для случая пары простых комплексно-сопряженных корней  , два решения , и ;

для случая пары - кратных комплексно-сопряженных корней  , решений:

, , …,,

, , …,;

Составляется линейная комбинация найденных решений, эта линейная комбинация с произвольными коэффициентами  даст общее решение уравнения в плоскости.

Решение дифференциального уравнения свободного движения САР

Дифференциальное уравнение свободного движения

Данное уравнение есть линейное, однородное дифференциальное уравнение четвертого порядка, с постоянными коэффициентами.

Решим данное дифференциальное уравнение для , .

При , , указанные выше условия устойчивости системы выполняются.

Вышеуказанному дифференциальному уравнению, соответствует характеристическое уравнение.

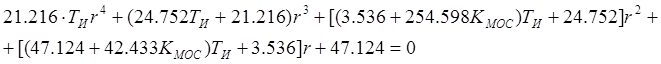
Данное характеристическое уравнение имеет четыре корня;

получим следующие корни

В случае простых комплексно-сопряженных корней, частные решения, соответственно:

,

,

,

.

Общее решение дифференциального уравнения есть линейная комбинация найденных решений:

, (*)

Решение задачи Коши

Начальные условия:

Слева:

Если допустить, что при  и САР работала в условиях установившегося равновесного режима, то:

; ; ; ; .

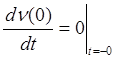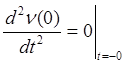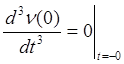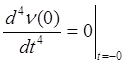Справа:

Однако, для решения задачи Коши, уравнения четвертого порядка, одного начального условия недостаточно, то я руководствовался следующими рассуждениями.

Так как, единичное возмущение подается на вход объекта, а выходная характеристика снимается с выхода объекта, то, предполагая, что в силу инерционности регулятора, в момент времени ,  поведение САР совпадает с поведением объекта,

Таким образом, начальные условия при могут быть определены из решения дифференциального уравнения динамики объекта:

.

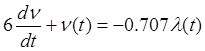Решение дифференциального уравнения динамики объекта:

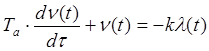
При исследовании единичного скачкообразного возмущения входного параметра  мы можем  считать  тождественно равным единице,  и уравнение принимает вид:

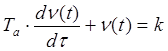
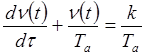
левая часть есть однородное дифференциальное уравнение

,

,

,

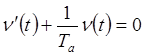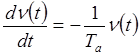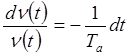
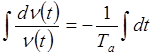
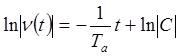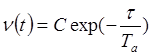, где ,

или ,

, (**)

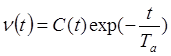продифференцируем по  уравнение (**),

,

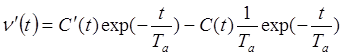и подставим в исходное уравнение,

,

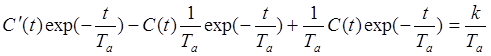после упрощения,

,

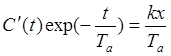или,

.

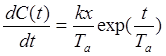Таким образом:

,

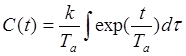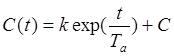, подставим в уравнение (**).

Получим,

,

,

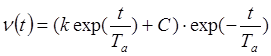При исследовании объекта допустим, что точке , функция,  непрерывна, т.е.,

 

Тогда очевидно, что ,

тогда

,

тогда для нашего случая, уравнение примет вид:

Соответственно:

;

;

;

Очевидно, что в момент времени t=+0,

;

;

;

;

Таким образом: начальные условия справа, при t=+0,

;

;

;

;

Дифференцируем уравнение (*), не показывая промежуточные преобразования в виду громоздкости, получим следующую систему уравнений:

,

,

,

,

где  и  - действительная и мнимая часть  корня соответственно.

Или

,

,

,

,

Определитель системы

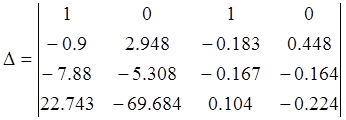
Т.к. определитель не равен нулю, то система имеет единственное решение

;

;

;

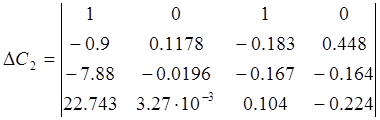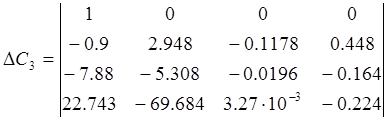Определим константы интегрирования:

; ; ; .

;

;

;

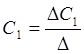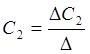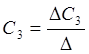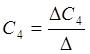Уравнение (**) примет вид:

; (***)

Таким образом, решение дифференциального уравнения движения САР, есть уравнение (***).

Переходной процесс в САР, будет выглядеть следующим образом:

 
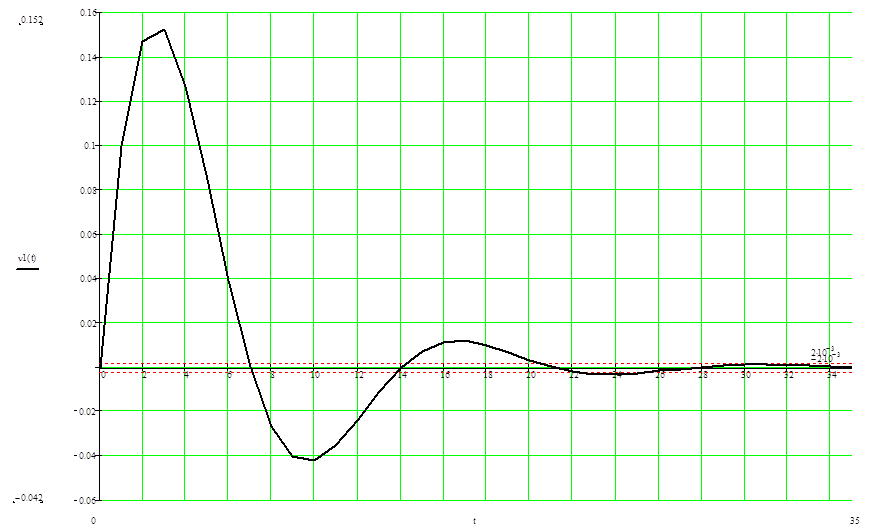
Переходной процесс в САР при совмещении с переходным процессом турбины, без регулятора:

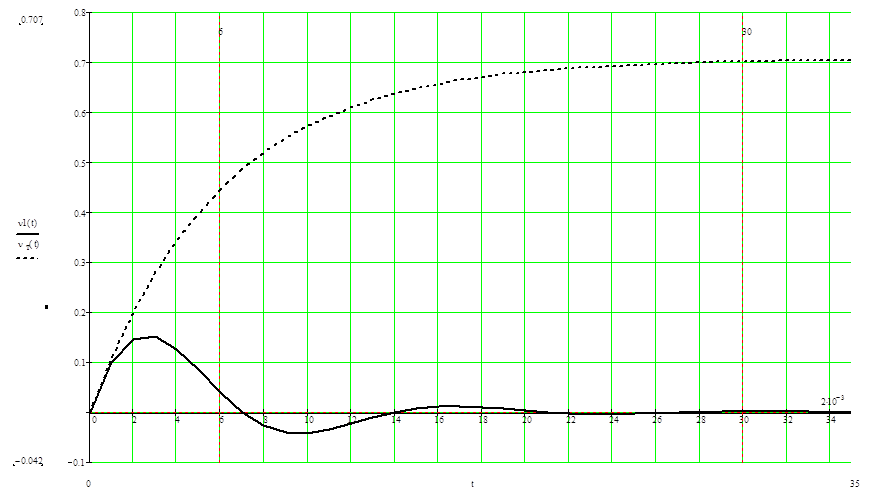
где, сплошная линия – переходной процесс турбины с САР;

пунктирная линия – переходной процесс турбины без регулятора.