Конвективный теплообмен. Дифференциальное уравнение конвективного теплообмена, страница 4

Теоретическое определение коэффициента теплоотдачи  возможно лишь для очень ограниченного числа простейших случаев. В инженерной практике пользуются расчетными зависимостями, полученными путем обобщения многочисленных экспериментальных данных на основе теории подобия. Для этого необходимо дифференциальное уравнение конвективного теплообмена.

17.3. Дифференциальное уравнение конвективного теплообмена

Для вывода дифференциального уравнения конвективного теплообмена в установившемся потоке жидкости (газа) выделяют элементарный параллелепипед с гранями dx, dy, dz (рис. 15.1) и составляют для него тепловой баланс, приняв физические параметры λ, с_р и ρ постоянными. Скорости движения жидкости в направлении осей x, y и z, соответственно – w_x, w_y и w_z. Температура жидкости t изменяется вдоль граней параллелепипеда. Теплоперенос в жидкости осуществляется путем конвекции и теплопроводности. Все подведенное к параллелепипеду тепло затрачивается только на изменение его энтальпии.

Количество тепла, которое вводится жидкостью путем конвекции по направлению оси х через грань dydz за время dτ,

                             .

За это же время через противоположную грань параллелепипеда путем конвекции жидкостью выводится количество тепла

       ,

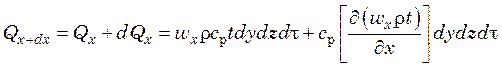или

       .

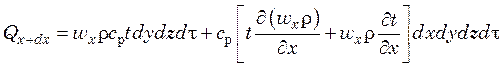Разность между количествами введенного и выведенного тепла в направлении оси х за время dτ составит:

          .

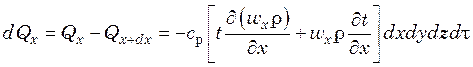Аналогично в направлении осей y и z

                   ;

                   .

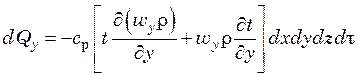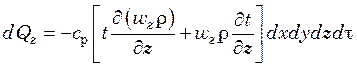Полная разность между количествами введенного и выведенного путем конвекции тепла в объеме параллелепипеда за время dτ

                     .

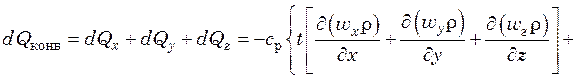
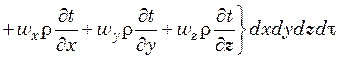На основании уравнения неразрывности потока

                          .

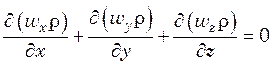Тогда конвективная составляющая теплового потока

                 ,

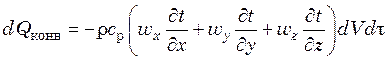где  – объем параллелепипеда.

Количество тепла, которое вводится в параллелепипед жидкостью путем теплопроводности за время dτ равно

                       .

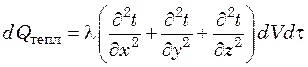Суммарное количество тепла, подведенное конвекцией и теплопроводностью

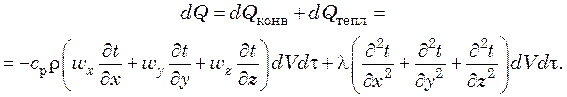
Это тепло dQ, согласно первому началу термодинамики, равно изменению энтальпии жидкости в объеме параллелепипеда

                                    .

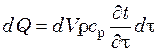Таким образом,

 .

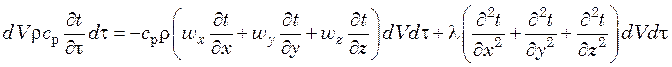В результате простейших преобразований последнего равенства, получим

            ,

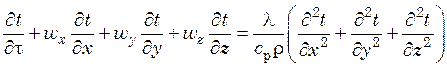либо

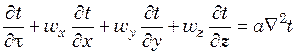                        ,                       (17.7)

где  – коэффициент температуропроводности.

Полученное уравнение (17.7) является дифференциальным уравнением конвективного теплообмена, или уравнением Фурье-Кирхгофа. Оно выражает в наиболее общем виде распределение температур в движущемся потоке жидкости (газа).

Для твердых тел w_x = w_y = w_z = 0 и уравнение (17.7) превращается в дифференциальное уравнение теплопроводности (15.23).

При установившемся процессе теплообмена 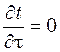, тогда уравнение конвективного теплообмена для этого случая

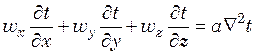                            .                          (17.8)

Ввиду сложности уравнения (17.7) для практического использования его подобно преобразовывают с учетом условий однозначности, т.е. представляют в виде функции от критериев подобия. Для этого, с целью более полного описания конвективного переноса тепла, дифференциальное уравнение Фурье-Кирхгофа дополняется граничными условиями, вытекающими из закона теплообмена на границе твердого тела и окружающей его среды.