Конвективный теплообмен. Дифференциальное уравнение конвективного теплообмена, страница 3

Интенсификация конвективного теплообмена связана с уменьшением толщины пограничного слоя. С развитием турбулентности пограничный слой может быть настолько тонким, что конвекция будет оказывать доминирующее влияние на теплообмен.

На размеры и структуру пограничного слоя оказывают влияние геометрическая форма и размеры поверхности теплообмена, которые определяют характер обтекания поверхности жидкостью или газом. В технике имеется большое многообразие поверхностей нагрева (пластины, трубы и т.д.), каждая из них создает специфические условия движения и теплоотдачи.

Малая толщина пограничного слоя позволяет пренебречь его кривизной (даже если стенка не является плоской) и считать температурный профиль в слое линейным. Это означает, что перенос теплоты через модельный тепловой пограничный слой можно рассматривать как теплопроводность через плоский слой жидкости или газа с теплопроводностью  и представить выражением

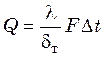                                        .                                       (17.2)

17.2. Уравнение теплоотдачи

Ввиду сложности механизма конвективного теплообмена и определения δ_т для удобства расчета теплоотдачи в основу его положен закон охлаждения Ньютона. Согласно этому закону теплоотдачи количество тепла dQ, передаваемое от поверхности теплообмена к окружающей среде или, наоборот, от окружающей среды к поверхности теплообмена, прямо пропорционально поверхности теплообмена dF, разности температур поверхности t_ст и окружающей среды t_ж и времени dτ, в течение которого осуществляется теплообмен, т.е.

                                 ,                               (17.3)

где  – коэффициент пропорциональности, который носит название коэффициента теплоотдачи.

Коэффициент теплоотдачи показывает, какое количество тепла передается от единицы поверхности нагрева в окружающую среду или, наоборот, от окружающей среды к единице поверхности теплообмена в единицу времени при разности температур теплообменной поверхности и окружающей среды в один градус:

                .

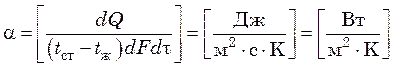При расчете конкретных установившихся тепловых процессов коэффициент теплоотдачи принимают постоянным вдоль всей теплообменной поверхности, тогда уравнение (17.3) принимает вид:

                              ,                             (17.4)

где Q – количество тепла, переносимое в единицу времени, Вт.

Сопоставление уравнений (17.2) и (17.4) для одного и того же потока теплоты дает соотношение

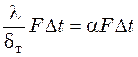                         ,   или 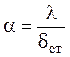  .                        (17.5)

Это соотношение, как правило, не является расчетным, так как за редким исключением толщина пограничного слоя δ_т неизвестна. Однако выражение (17.5) позволяет моделировать явления конвективного переноса теплоты. Из этого выражения следует, что коэффициент теплоотдачи зависит от теплопроводности жидкости (газа), омывающей поверхность теплообмена, и толщины теплового пограничного слоя, который в свою очередь зависит от геометрической формы, размера и состояния (шероховатости) поверхности, ее температуры, характера и режима движения жидкости или газа, их физических и теплофизических свойств, а также коэффициента объемного расширения b. Таким образом, коэффициент теплоотдачи является функцией многих переменных:

                                                          (17.6)

где d и L – характерные линейные размеры (диаметр и длина соответственно); ε – степень шероховатости поверхности теплообмена.