сопротивления трения и, как правило, несколько местных сопротивлений полная потеря напора hпот является суммой двух слагаемых:
hпот = hтр + hм. (6.14)
Сопротивление трения подчиняется различным законам в зависимости от того, в каком режиме движения находится поток.
В случае ламинарного режима при движении жидкости по прямой трубе круглого сечения потеря напора на трение может быть определена теоретически.
В соответствии с уравнением Бернулли, для горизонтального трубопровода постоянного сечения напор, теряемый на трение
![]()
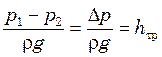
При
подстановке ![]() в уравнение Пуазейля, получим
в уравнение Пуазейля, получим
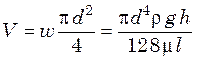 ,
,
откуда, после сокращений, находим потерянный напор
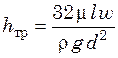 .
.
Умножая числитель и знаменатель правой
части на ![]() и группируя величины, окончательно получим
и группируя величины, окончательно получим
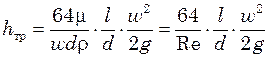 .
.
Таким образом, при ламинарном движении по прямой круглой трубе
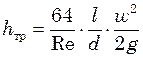 , (6.15)
, (6.15)
т.е. потерянный на трение напор
выражается через скоростной напор ![]() . Величину,
показывающую во сколько раз напор, потерянный на трение, отличается от
скоростного напора, называют коэффициентом сопротивления трения и обозначают
. Величину,
показывающую во сколько раз напор, потерянный на трение, отличается от
скоростного напора, называют коэффициентом сопротивления трения и обозначают ![]() , а отношение
, а отношение ![]() ,
входящее в эту величину, – коэффициентом гидравлического трения, или
просто коэффициентом трения, и обозначают
,
входящее в эту величину, – коэффициентом гидравлического трения, или
просто коэффициентом трения, и обозначают ![]() .
Поэтому
.
Поэтому
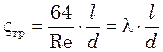 . (6.16)
. (6.16)
Следовательно, уравнение (6.15) может быть представлено в виде
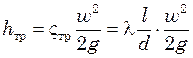 (6.17)
(6.17)
или для потери давления, учитывая что (![]() )
)
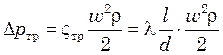 . (6.18)
. (6.18)
Для каналов некруглого сечения в
последние уравнения вместо диаметра ![]() подставляют
эквивалентный диаметр канала
подставляют
эквивалентный диаметр канала ![]() , причем
, причем
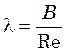 , (6.19)
, (6.19)
где В – коэффициент, величина которого зависит от формы поперечного сечения канала (для квадрата В = 57, кольца В = 96 и т.д.)
При ламинарном режиме движения, коэффициент трения l зависит только от величины критерия Рейнольдса, а потеря напора пропорциональна скорости потока в первой степени.
При
турбулентном режиме величина коэффициента l
зависит не только от критерия Рейнольдса, но и от шероховатости стенок трубы,
которую оценивают по степени шероховатости: 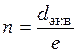 . Здесь
dэкв – эквивалентный диаметр трубопровода, а
. Здесь
dэкв – эквивалентный диаметр трубопровода, а ![]() – средняя высота выступа
шероховатости на внутренней поверхности трубы, м, т.е. абсолютная шероховатость.
– средняя высота выступа
шероховатости на внутренней поверхности трубы, м, т.е. абсолютная шероховатость.
Выражение для коэффициента трения при турбулентном режиме движения жидкости получить аналитическим путём невозможно из-за сложности структуры турбулентного потока. Поэтому расчётные уравнения для определения l получают обобщением результатов экспериментов.
Для расчёта коэффициента трения при турбулентном режиме может быть использована формула Альтшуля:
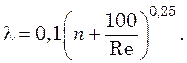 (6.20)
(6.20)
В случае гладких труб l может быть рассчитан по уравнению Блазиуса (в пределах Re = 104÷105)
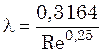 (6.22)
(6.22)
В случае гладких труб l может быть рассчитан по уравнению Блазиуса (в пределах Re = 104÷105)
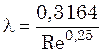 (6.22)
(6.22)
|
Рисунок 6.1 – Схемы сложных трубопроводов: а – параллельные; б – разветвленный; в – кольцевой |
либо по уравнению Никурадзе (в пределах Re = 105 – 3×106)
![]() . (6.23)
. (6.23)
Местные сопротивления по конструктивному признаку подразделяют на следующие виды :
1) внезапное и плавное расширение и сужение трубопровода в местах изменения его сечения;
2) фасонные части, в которых происходит изменение направления движения жидкости (отводы, колена);
3) фасонные части, в которых происходит деление или слияние потоков (тройники, крестовины);
4) арматура различного назначения (вентили, краны, задвижки, диафрагмы).
Потери напора на преодоление местных сопротивлений
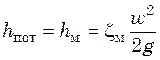 , (6.24)
, (6.24)
где zм – коэффициент местного сопротивления.
Если на трубопроводе имеется ряд местных сопротивлений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.