РАЗДЕЛ I ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
ЛЕКЦИЯ 3
Гидравлика. Основы гидростатики
Основные свойства жидкостей в гидравлике.
Дифференциальное уравнение равновесия жидкости Эйлера.
Основное уравнение гидростатики.
Практические приложения основного уравнения гидростатики.
В многочисленных производствах самых разных отраслей промышленности приходится встречаться с жидкостями, которые необходимо транспортировать, хранить, перемешивать, подвергать очистке, нагревать, испарять, диспергировать и т.д. Все эти процессы требуют аппаратно-технологического оформления, что невозможно без знания законов равновесия и движения жидкостей. Эти законы рассматриваются в науке, которая носит общее название «Механика жидкости» и подразделяется на «Статику жидкости» («Гидростатику») и «Динамику жидкости» («Гидродинамику»); в ней даются также способы практического приложения этих законов, т.е. разрабатываются соответствующие методы гидромеханических расчетов различных процессов, конструкций и устройств.
3.1. Основные определения.
Под жидкостью подразумевают физическое тело которое:
а) незначительно изменяет свой объём при изменении давления и температуры (в этом жидкость сходна с твердым телом);
б) обладает текучестью, благодаря чему не имеет собственной формы и принимает форму того сосуда, в котором находится (в этом жидкость сходна с газом).
Поскольку газ также обладает свойством текучести, то многие теоретические положения, разработанные по отношению к жидкому телу, могут быть распространены на газообразные тела.
В гидравлике принято объединять жидкости, газы и пары под единым наименованием – жидкости. При аналитических исследованиях часто пользуются понятием «идеальной» жидкости, которая в отличие от реальной жидкости, абсолютно несжимаема под действием давления, не изменяет плотности при изменении температуры и не обладает вязкостью.
Реальные жидкости делятся на капельные (жидкости в обычном смысле этого слова) и вязкоупругие (газы и пары).
3.2. Основные физические свойства жидкостей
Плотность,
удельный объем и удельный вес. Масса единицы объема жидкости называется
плотностью и обозначается ![]() :
:
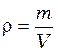 , (3.1)
, (3.1)
где m – масса жидкости, кг; V – объем жидкости, м3.
Следовательно, размерность плотности кг/м3.
В расчетах часто пользуются понятием относительной плотности жидкости, т.е. отношением плотности жидкости к плотности воды при 4 °С.
Плотность смеси жидкостей, при которых не происходит существенных физико-химических изменений, приближенно можно рассчитать, принимая, что объем смеси равен сумме объемов компонентов:
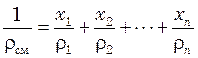 , (3.2)
, (3.2)
где ![]() – массовые доли компонентов смеси;
– массовые доли компонентов смеси; ![]() – плотность смеси и ее компонентов.
– плотность смеси и ее компонентов.
Объем,
занимаемый единицей массы, или величина обратная плотности, называется удельным
объемом и обозначается ![]() :
:
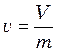 . (3.3)
. (3.3)
Размерность удельного объема м3/кг.
Вес единицы
объема жидкости называется удельным весом и обозначается ![]() :
:
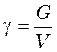 , (3.4)
, (3.4)
где ![]() – вес жидкости, Н
– вес жидкости, Н
![]() , (3.5)
, (3.5)
где ![]() – ускорение свободного падения, м/с2.
– ускорение свободного падения, м/с2.
Соотношение между удельным весом и плотностью:
![]() . (3.6)
. (3.6)
Аналогично относительной плотности относительным удельным весом жидкости называется отношение удельного веса жидкости к удельному весу воды при 4 °С.
Плотность газов приближенно может быть рассчитана по уравнению состояния идеальных газов Менделеева-Клапейрона:
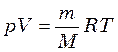 , (3.7)
, (3.7)
где ![]() – давление, Па;
– давление, Па; ![]() – молекулярная масса газа, кг/кмоль;
– молекулярная масса газа, кг/кмоль; ![]() – универсальная газовая постоянная,
– универсальная газовая постоянная, ![]() Дж/(кмоль·К).
Дж/(кмоль·К).
Из этого уравнения следует, что:
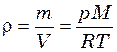 . (3.8)
. (3.8)
Для
приближенных расчетов плотность газов и паров при произвольном давлении и
температуре ![]() может быть определена по формуле:
может быть определена по формуле:
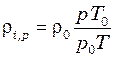 , (3.9)
, (3.9)
где ![]() – плотность при нормальных условиях,
(нормальные условия
– плотность при нормальных условиях,
(нормальные условия ![]() =0ºС и
=0ºС и ![]() =760
мм.рт.ст.=1,013·105 Па).
=760
мм.рт.ст.=1,013·105 Па).
Плотность смеси газов с достаточной степенью точности может быть рассчитана:
![]() (3.10)
(3.10)
где![]() –
объемные доли компонентов смеси;
–
объемные доли компонентов смеси; ![]() – соответствующие
плотности компонентов.
– соответствующие
плотности компонентов.
Сжимаемость жидкости характеризуют коэффициентом сжимаемости bV, Па–1.
Коэффициент сжимаемости bV равен отношению изменения относительного
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.