Моделирование объектов систем компьютерного управления; сбор и фиксация результатов моделирования. Вариант № 2, страница 3

4.1.3.  Зависимости при  a₁ = 1,4.

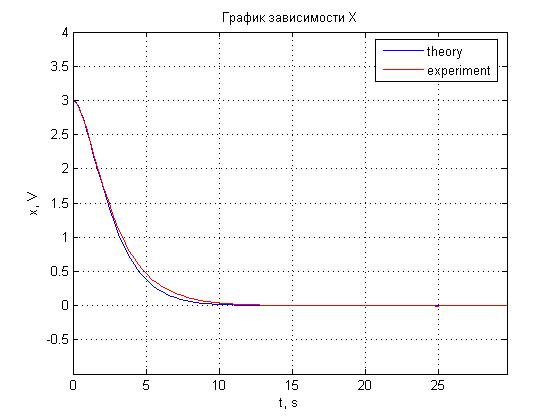
Рис. 4.7. График зависимости x(t).

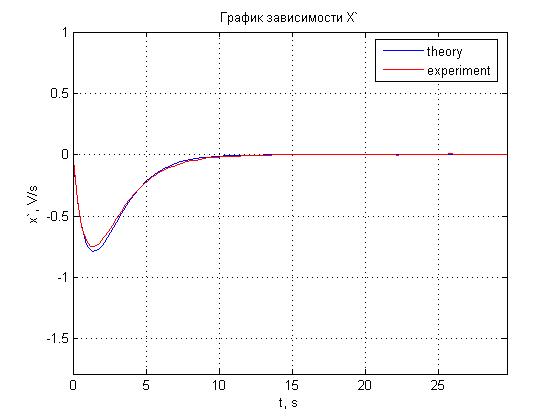
Рис. 4.8. График зависимости x'(t).

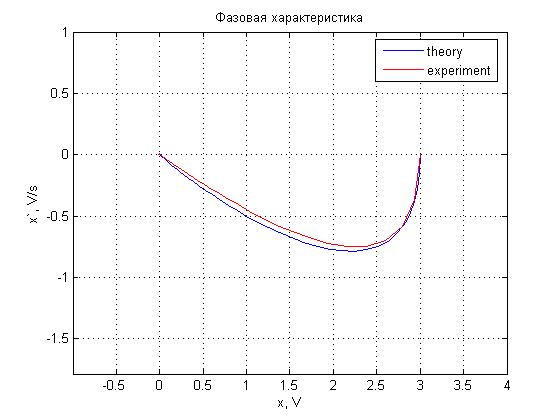
Рис. 4.9. Фазовая характеристика

4.1.4. Зависимости при  a₁ = 3.

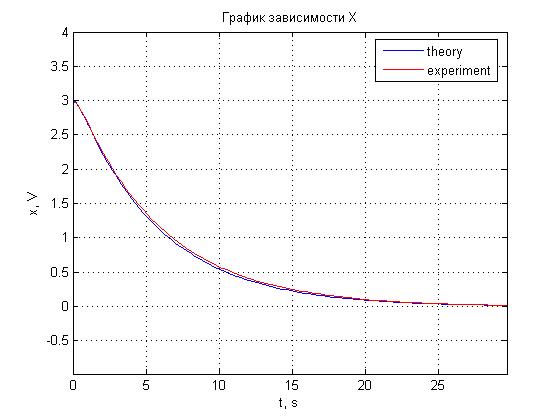
Рис. 4.10. График зависимости x(t).

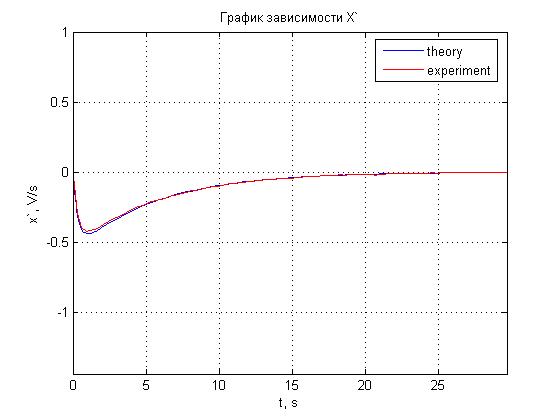
Рис. 4.11. График зависимости x'(t).

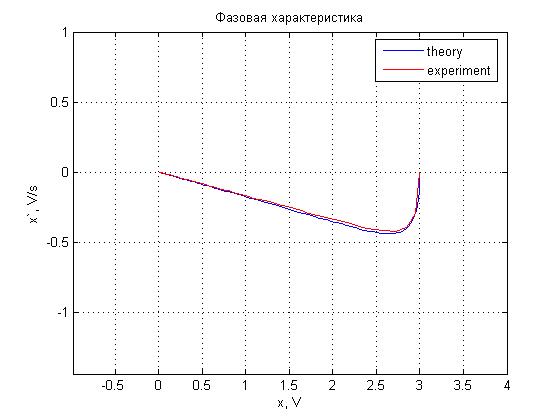
Рис. 4.12. Фазовая характеристика.

4.2.  

4.2.1. Зависимости при  a₁ = 0.

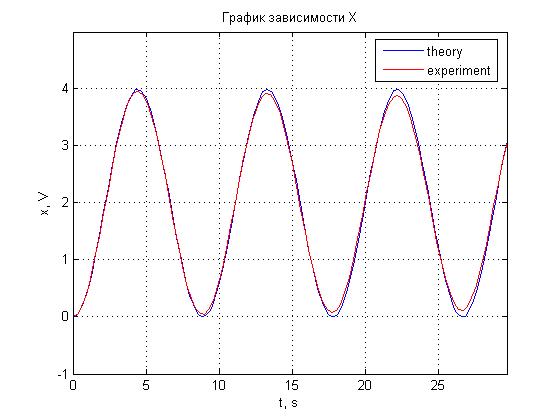
Рис. 4.13. График зависимости x(t).

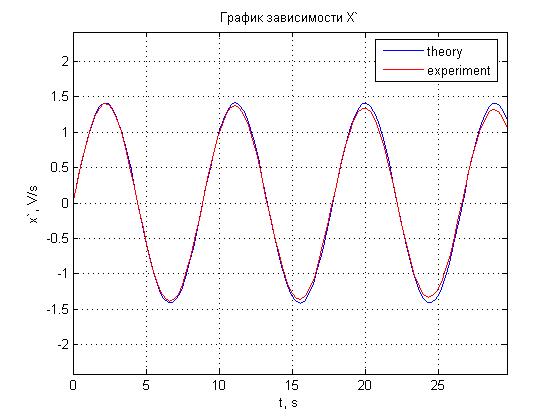
Рис. 4.14. График зависимости x'(t).

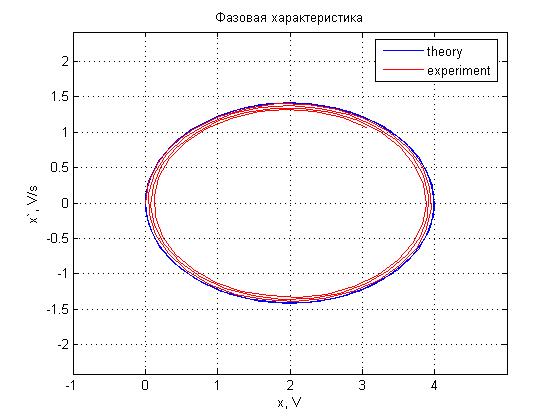
Рис. 4.15. Фазовая характеристика.

4.2.2. Зависимости при  a₁ = 1.

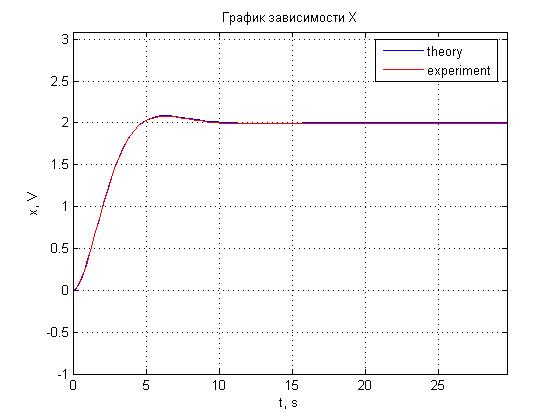
Рис. 4.16. График зависимости x(t).

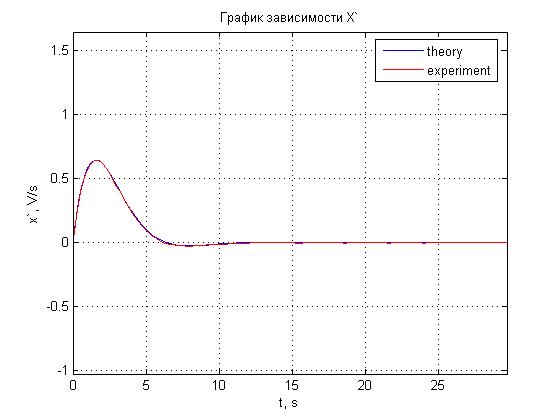
Рис. 4.17. График зависимости x'(t).

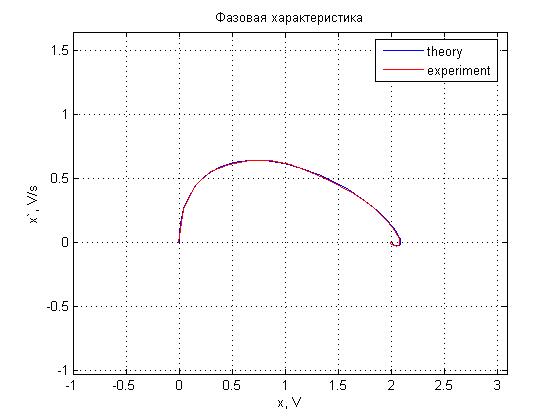
Рис. 4.18. Фазовая характеристика.

4.2.3. Зависимости при  a₁ = 1,4:

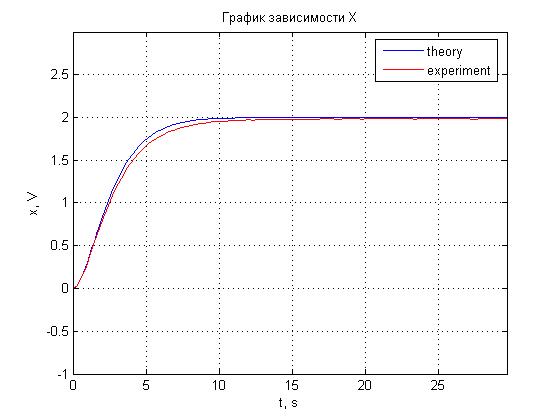
Рис. 4.19. График зависимости x(t).

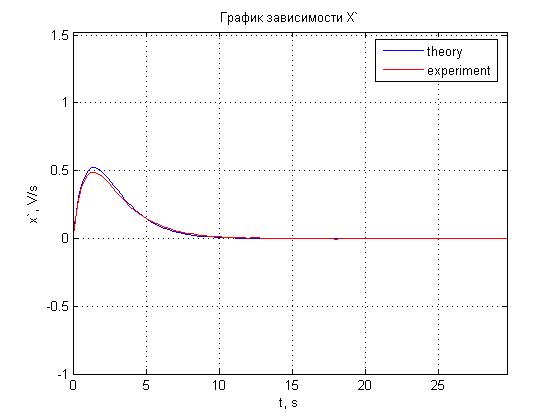
Рис. 4.20. График зависимости x'(t).

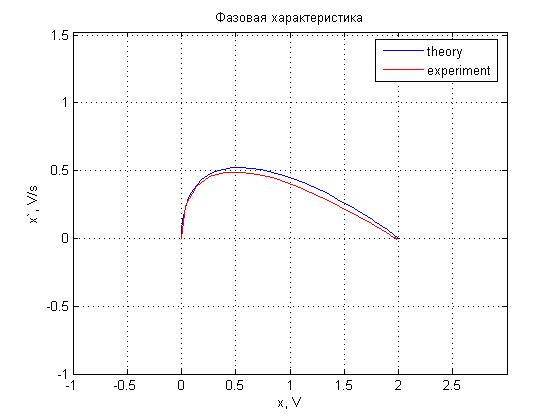
Рис. 4.21. Фазовая характеристика.

4.2.4. Зависимости при  a₁ = 3:

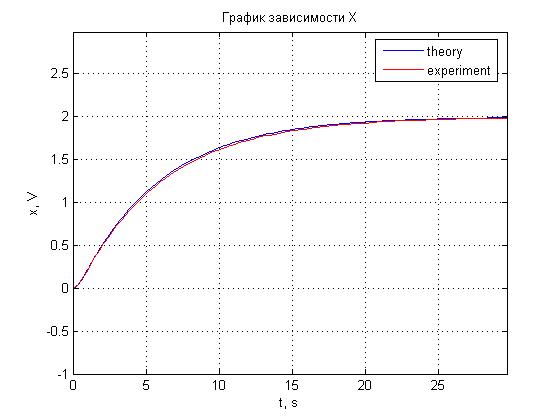
Рис. 4.22. График зависимости x(t).

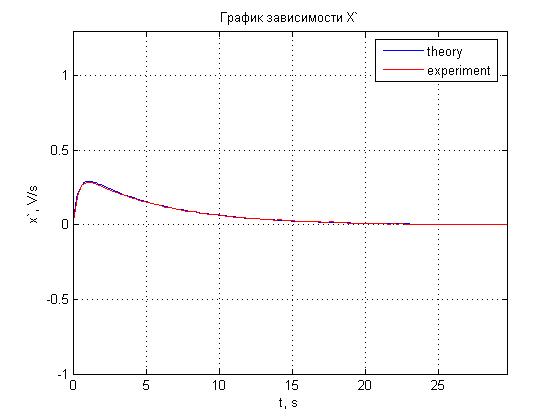
Рис. 4.23. График зависимости x'(t).

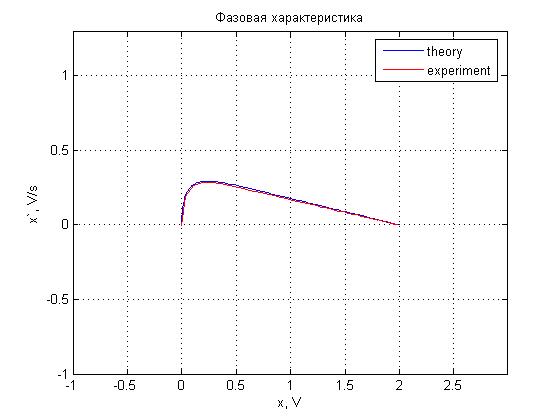
Рис. 4.24. Фазовая характеристика.

5. Выводы

В данной лабораторной работе с помощью АВК-31 моделировалось поведение объекта, заданного  линейным дифференциальным уравнением второго порядка. Эксперименты показали, что результаты моделирования довольно точно совпадают с теоретическими. Имеющиеся расхождения вызваны прежде всего отклонением аналоговых элементов от их номиналов. Также необходимо заметить, что как только коэффициент в линейном дифференциальном уравнении перед x', отвечающий за демпфирование колебаний становится равен нулю, колебания не затухают. При увеличении коэффициента демпфирования колебания затухают все сильнее, что при определенном значении приводит к апериодическому процессу. В точке бифуркации система находится в неопределенном состоянии, при котором сложно спрогнозировать колебательность системы.