Моделирование объектов систем компьютерного управления; сбор и фиксация результатов моделирования. Вариант № 2, страница 2

Рис.3.2. Схема набора.

4.Теоретические расчеты и экспериментальные данные

Найдем точку бифуркаций для заданного диффиринциального уравнения:

 

Необходимо найти такое a₁ при котором дискриминант следующего уравнения будет равен нулю:

 

Найдем решение

 ,

Тогда , при     =>   

Для решения дифференциального уравнение преобразуем его к системе

Сделаем необходимую замену:           

                 

     

Тогда уравнение можно приобразовать к системе следующего вида:

 

   

Зададим систему как функцию в Matlab

function dy = f(t,y)     v = 0; %2     a0 = 0.5;     a1 = 0; %1 3     dy = zeros(2,1);     dy(1) = y(2);     dy(2) = a0*v-a1*y(2)-a0*y(1); end

Для решения системы был реализован следующий скрипт:

function paint()    close all    y0 = [3 0]; % [0 0]    ts = [0 30];    [t, y] = ode45('f', ts, y0);    % график У    plot(t, y(:,1));    axis( [ min(t), max(t), min(y(:,1))-1, max(y(:,1)+1) ] )    title('Diagram X');    xlabel('t, s'); ylabel('x, V');    grid on    % график производной    figure    plot(t, y(:,2));    axis( [ min(t), max(t), min(y(:,2))-1, max(y(:,2)+1) ] )    title('Diagram X’');    xlabel('t, s'); ylabel('x`, V/s');    grid on    % фазовая    figure    plot(y(:,1), y(:,2));    axis( [ min(y(:,1))-1, max(y(:,1)+1) , min(y(:,2))-1, max(y(:,2)+1) ] )    title('Phase');    xlabel('x, V'); ylabel('x`, V/s');    grid on end

Все необходимые параметры задаются в скриптах, скрипт paint.m строит 3 графика: график зависимости Х, график зависимости Х’ и фазовую характеристику.

Решим систему для различных начальных условий

4.1  

4.1.1 Зависимости при  a₁ = 0:

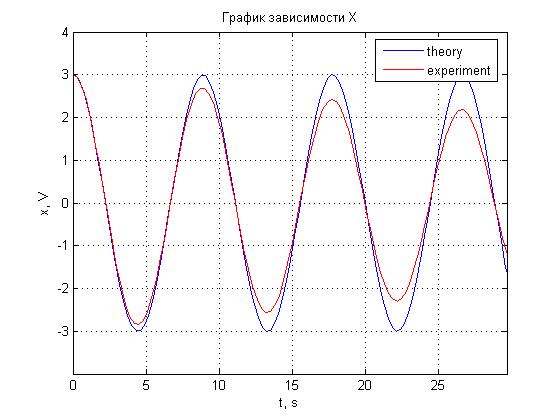
Рис. 4.1. График зависимости x(t).

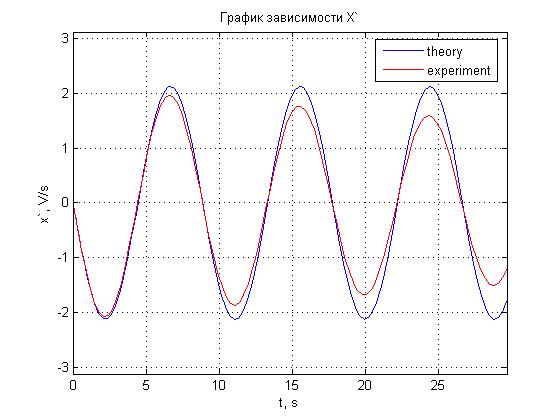
Рис. 4.2. График зависимости x'(t).

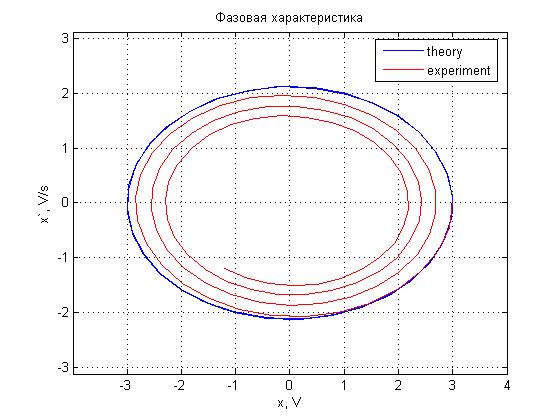
Рис. 4.3. Фазовая характеристика.

4.1.2.  Зависимости при  a₁ = 1.

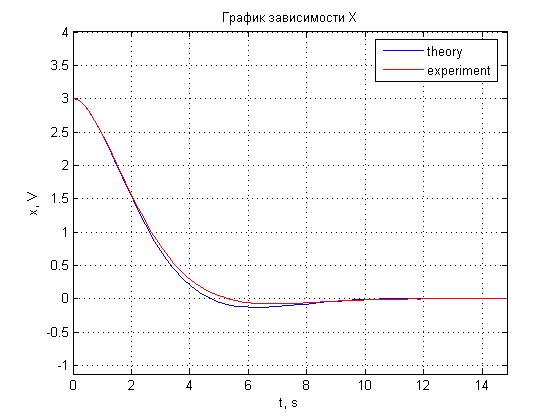
Рис. 4.4. График зависимости x(t).

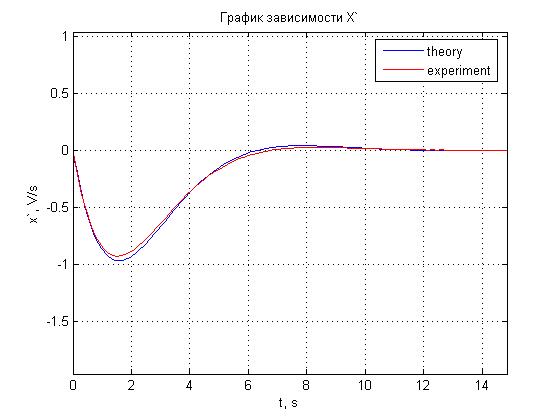
Рис. 4.5. График зависимости x'(t).

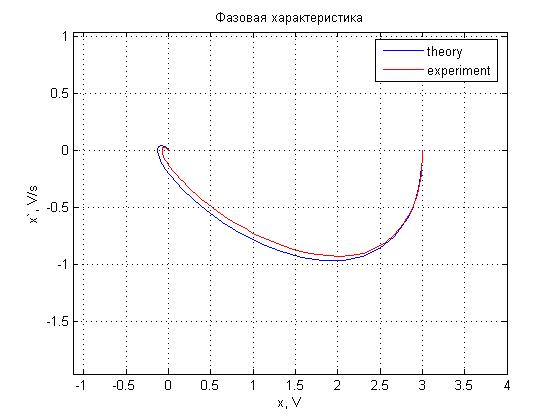
Рис. 4.6. Фазовая характеристика