Эконометрическая модель с зависимостью между чистым доходом и объемом капиталовложений в экономику страны, страница 4

При уровне значимости = 0,05 и n = 8, определяется верхняя и нижняя граница:

Нижняя граница DW₁ = 0,94

Верхняя граница DW₂ = 1,29

Поскольку DW_факт < DW₁ , можно утверждать, что неучтенные остатки имеют дополнительную автокорреляцию.

Если DW_факт  > DW₂ – принимается гипотеза про отсутствие автокорреляции. Если DW₁ < DW_факт < DW₂ – конкретных выводов сделать нельзя, необходимо дальше проводить исследование, беря большую совокупность наблюдений.

Автокорреляция – это взаимосвязь последовательных элементов временного или пространственного ряда данных.

Найдем критерий Фишера, для чего рассчитаем остаточную и общую дисперсию.

Остаточная дисперсия:

Общая дисперсия:

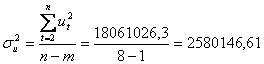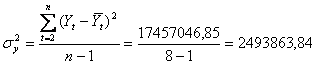Год	Ŷt	(Yt – Ỹt)2
1	1132,37	2296782,684
2	1367,34	2238719,175
3	1507,74	2204381,6
4	1484,30	2210095,516
5	1540,38	2196436,633
6	1685,10	2161382,186
7	1962,82	2094900,18
8	2134,39	2054348,89
∑	12814,44	17457046,85

Ỹ_t = ∑ Ŷ_t   / 8 = 1601,81.

Найдем критерий Фишера:

Fтабл = 4,46

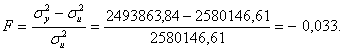Fфакт < Fтабл.

Вывод: Значение коэффициента детерминации свидетельствует о том, что на 3996,1% вариация чистого дохода определяется вариацией капиталовложений. Коэффициент корреляции (6,32) свидетельствует о достаточно тесной связи между капиталовложениями и чистым доходом. Величина критерия Дарбина – Уотсона говорит о наличии дополнительной автокорреляции остатков модели. Также рассчитанные характеристики свидетельствуют о значимости связи между капиталовложениями и чистым доходом в период t-1.