Розрахунок та проектування приводу головного руху верстата I групи, страница 3

4.1  Графоаналітичний метод розрахунку приводу

головного   руху

Цей метод полягає в будівництві  двох графіків:

1               1) структурна сітка, яка дає можливість визначити відносну залежність передаточних відношень в кожній групі передач;

2) графіка частот, який дає можливість визначити абсолютні величини передаточних відношень всіх передач коробки швидкостей.

Розглянемо розрахунок приводу головного руху, який включає коробку швидкостей з одним зв’язаним колесом і реверсивним механізмом. Привод головного руху включає двигун (М) з визначеними параметрами, пасову передачу (d₁-d₂) і коробку швидкостей, яка забезпечує зміну обертання шпинделя верстата. При вмиканні електромагнітної муфти ЕМВ шпиндель обертається за годинниковою стрілкою, а при вмиканні муфти ЕМН шпиндель обертається проти годинникової стрілки.

Коробка швидкостей має три групи передач по дві передачі в кожній групі і структурну формулу 10=2∙5 і таким чином забезпечує вісім різних частот обертання шпинделя .

Позначимо  передаточні відношення усіх передач:

пасової

реверсивного механізму

Першої групи

 

Другої групи

    

Для кінематичного розрахунку передаточне відношення реверсивного механізму приймаємо рівним одиниці.

Для коробки швидкостей, яка має три групи, визначаємо кількість можливих варіантів

B=m! =2! =1∙2=2

Запишемо розгорнуті структурні формули для кожного варіанту:

перший варіант 10=2[1]∙5[2];

другий варіант 10=2[5]∙5[1];

За розгорнутими структурними формулами будуємо структурні сітки і перевіряємо на виконання двох умов: можливість конструктивного здійснення; можливість отримання мінімальних габаритів, при цьому знаменник ряду швидкостей φ=1.26

Для першого варіанту:

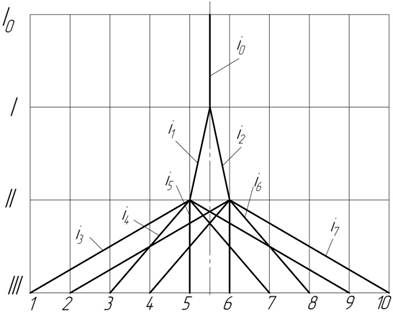
(D_і)_1гр=і₂/і₁=φ    (D_і)_2гр=і₇/і₃=φ⁸   

(D_і)_max≤8→(D_і)_max=(D_і)_2гр=φ⁸=1.26⁸≤8

(D_і)_1гр<(D_і)_2гр=φ<φ⁸

Обидві вимоги виконуються

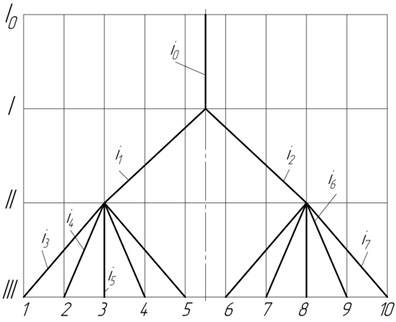
Для другого варіанту:

(D_і)_1гр=і₂/і₁=φ⁵    (D_і)_2гр=і₇/і₃=φ⁴   

(D_і)_max≤8→(D_і)_max =(D_і)_1гр=φ⁵=1.26⁵≤8

(D_і)_1гр<(D_і)_2гр=φ⁵<φ⁴

Друга вимога не виконується

Співвідношення варіантів показує, що кращім є перший варіант, оскільки він повністю задовольняє двом умовам. Для нього будуємо графік частот. При побудові графіка частот обираємо положення крапки  n₀=n₈      в межах високих ступенів і визначаємо загальне мінімальне передаточне відношення коробки швидкостей, яке дорівнює добутку мінімальних передаточних відношень кожної групи  передач

І_kc= і₃∙і₁=1/φ⁹

Отриману ступінь при φ розбиваємо між min передаточним відношенням задовольняють двом умовам:

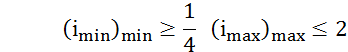
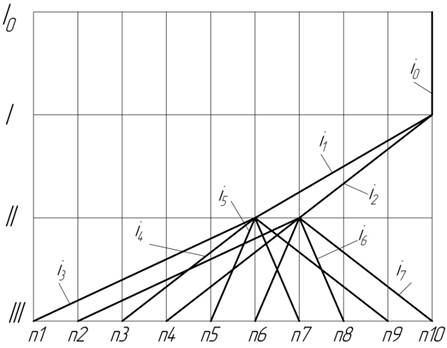
Рис.4.1 Графік частот обертання шпинделя.

На основі отриманого графіка частот записуємо передаточні відношення по групам:

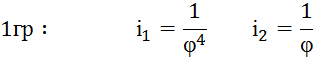
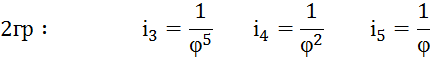
Обидві вимоги виконані.

4.2   Визначення чисел зубцівусіх передач коробки швидкостей

Число зубів коробки швидкостей є параметри передач коробки швидкостей. Число зубів коробки швидкостей визначають по групам.

Задамо значення чисел зубів відомого мінімального колеса. В цьому випадку  для першої групи Z1 у межах від 18 до 20 і розв'язуємо систем трьох рівнянь з трьома невідомими.

Визначаємо невідомі

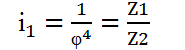
Z1+Z2=Z3+Z4

Задамо значення чисел зубів відомого мінімального колеса. В цьому випадку для другої групи Z5 в межах від 20 до 22. Розв'язуючи систему трьох рівнянь з трьома невідомими. Визначаємо невідомі

     

   

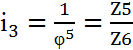
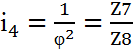
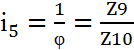
Z5+Z6=Z7+Z8

Z7+Z8=Z9+Z10

Z9+Z10=Z11+Z12

Z11+Z12=Z13+Z14

Що стосується чисел зубів коробки швидкостей реверсивного механізму, то їх визначаємо конструктивно, тобто передаточне відношення реверсивного механізму приймають рівним одиниці

I₀=Z1/Z2=1      Z1+Z2≤100

Отриманні значення чисел зубів усіх коліс записуємо в таблицю 4.1 чисел зубів коробки швидкостей  

Таблиця 4.1 Числа зубів коробки швидкостей

Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9	Z10	Z11	Z12	Z13	Z14
18	45	21	42	20	64	28	56	37	47	47	37	56	28

4.3   Розрахунок параметрів постійних передач у ланцюзі приводу головного руху