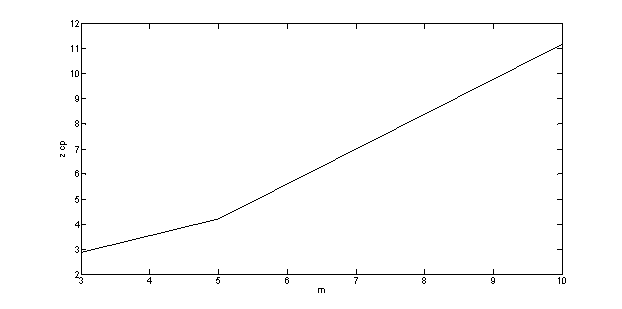
Рис. 19. Зависимость zсp =f(m)
Качество фильтрации не зависит от величины шума и частоты дискретизации, но зависит от параметров фильтра.
IV. Исследование работы фильтров при полезном входном сигнале в условиях помех.
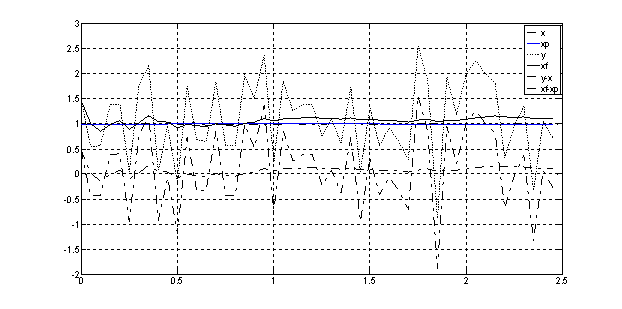
Рис. 20. Переходный процесс х(t) = f(t) при зашумленном постоянном сигнале, поданном на первый фильтр
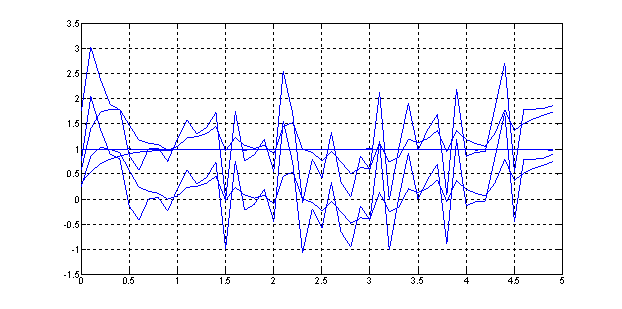
Рис. 21. Переходный процесс х(t) = f(t) при зашумленном постоянном сигнале, поданном на второй фильтр
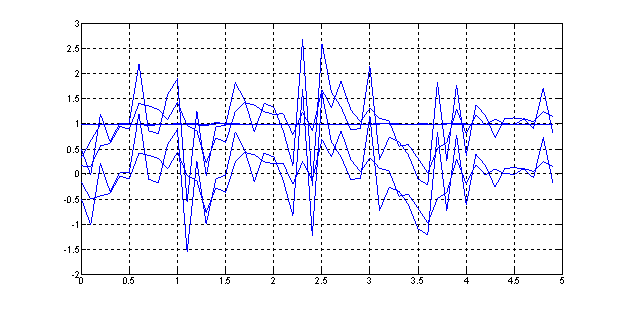
Рис. 22. Переходный процесс х(t) = f(t) при зашумленном постоянном сигнале, поданном на третий фильтр
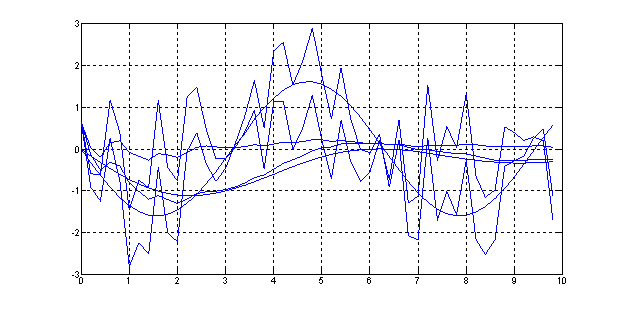
Рис. 23. Переходный процесс х(t) = f(t) при зашумленном гармоническом сигнале, поданном на первый фильтр
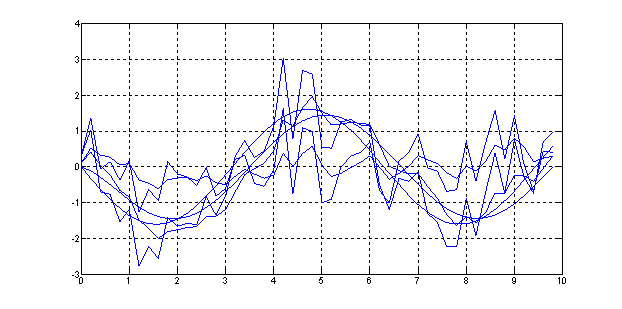
Рис. 24. Переходный процесс х(t) = f(t) при зашумленном гармоническом сигнале, поданном на второй фильтр
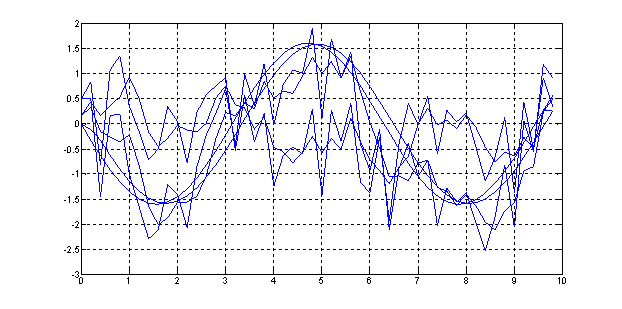
Рис. 25. Переходный процесс х(t) = f(t) при зашумленном гармоническом сигнале, поданном на третий фильтр
Анализ результатов и выводы:
Полученные в процессе работы экспериментальные зависимости показали, что Фильтр с бесконечной памятью лучше других фильтрует «белый шум», но при этом
неприменим для фильтрации динамических сигналов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.