Исследование рекуррентных алгоритмов цифровой фильтрации сигналов методом усреднения. Вариант № 2, страница 3

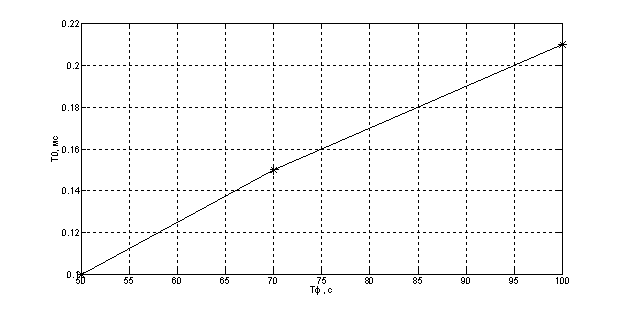
Рис. 8. Зависимость Тф=f(T0)

Постоянная времени возрастает  линейно при увеличении периода квантования и глубины памяти.

II.  Исследование работы фильтров при гармоническом входном сигнале.

1)  Первый фильтр

Не годится для фильтрации синусоидального сигнала, так как коэффициент передачи стремится к нулю (интеграл от синуса стремится к нулю). Фаза = п/2.

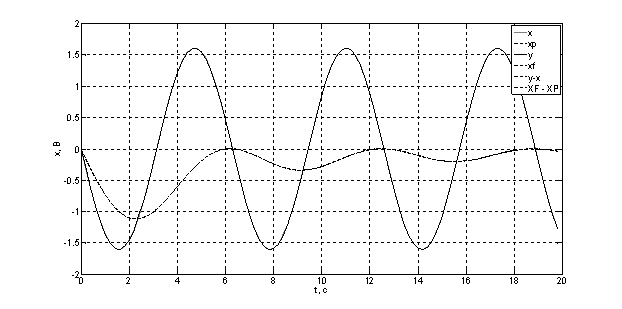
Рис. 9. Переходный процесс при подаче на первый фильтр гармонического сигнала.

2)  Второй фильтр

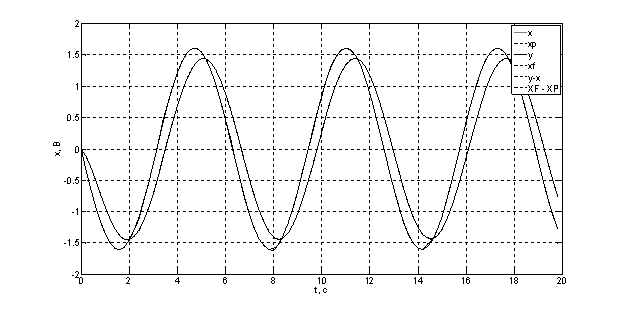
Рис. 10. Переходный процесс при подаче на второй фильтр гармонического сигнала.

Основные параметры выходной величины от присутствия н.у. не зависят.

Таблица 5. Зависимость фазы и коэффициента передачи от коэффициента коррекции(N1)

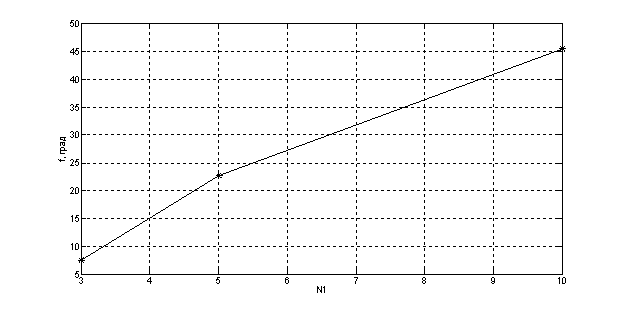
Рис. 11. Зависимость Ψ =f(N1)

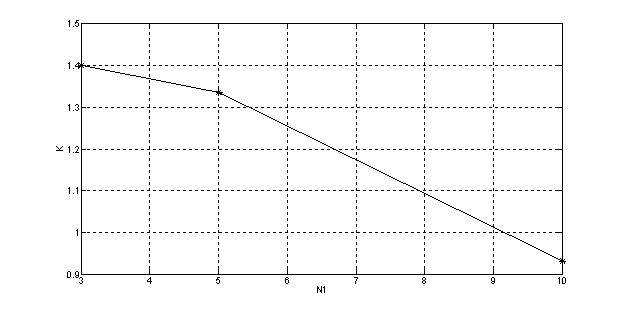
Рис. 12. Зависимость K =f(N1)

Таблица 6. Зависимость фазы и коэффициента передачи от от периода квантования(T0)

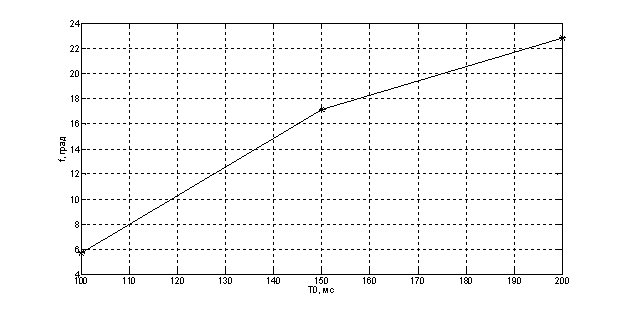
Рис. 13. Зависимость Ψ =f(T0)

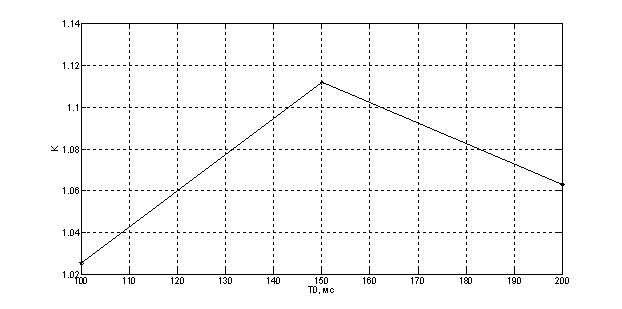
Рис. 14. Зависимость K =f(T0)

Фаза возрастает при увеличении N1 и Т0, коэффициент уменьшается при возрастании N1, а от Т0 не зависит.

3)  Третий фильтр

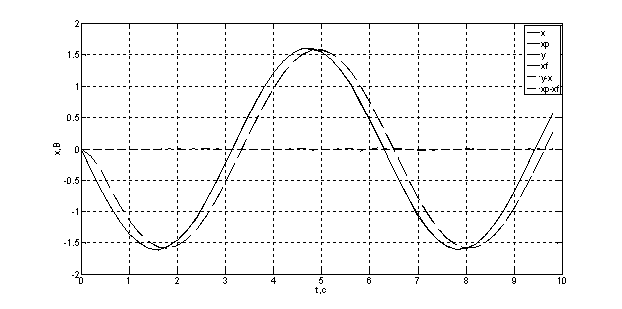
Рис. 15. Переходный процесс при подаче на третий фильтр гармонического сигнала.

Таблица 8. Зависимость фазы и коэффициента передачи от коэффициента коррекции(m)