Эластогидродинамическая задача трения в кулачковых механизмах: Методические указания к практической работе № 7 по дисциплине «Триботехника», страница 2

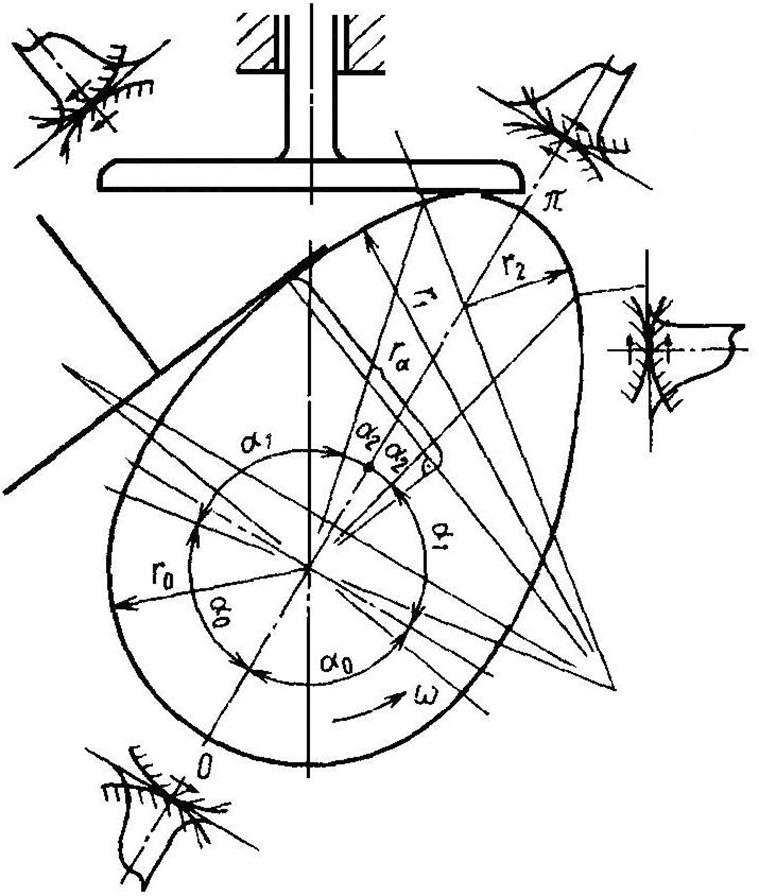
В рассматриваемом случае на отдельных участках контура кулачка a₀, a₁ и a₂ его кривизна определяется радиусами r₀, r₁ и r₂. Обе поверхности перемещаются относительно точки контакта со скоростью движения по ним точки:

u₀ = u_{1 t} = u _{2 t} = wr.

Кроме того, возникает скорость скольжения относительно точки контакта, определяемая формулой u₃ = – wr_a. В результате гидродинамическую скорость можно определить зависимостью:

.

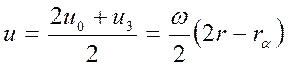Для угла – a₀ < a < a₀ на дуге покоя, где Т = Т_a = Т₀ имеет место чистое скольжение кулачка по толкателю, скорость

.

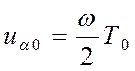Для угла a = a₁ = a₃ характерно качение со скольжением, где скорость скольжения меньше и противоположна скорости качения. Гидродинамическая скорость

.

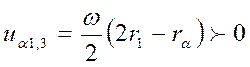На границе между углами a₁ и a₂, а также a₂ и a₃ чаще всего происходит изменение направления гидродинамической скорости и изменяется направление щели, образующей ЭГД-пленку смазки (рис. 2.1). Гидродинамическая скорость для угла

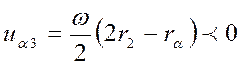.                                   (2.1)

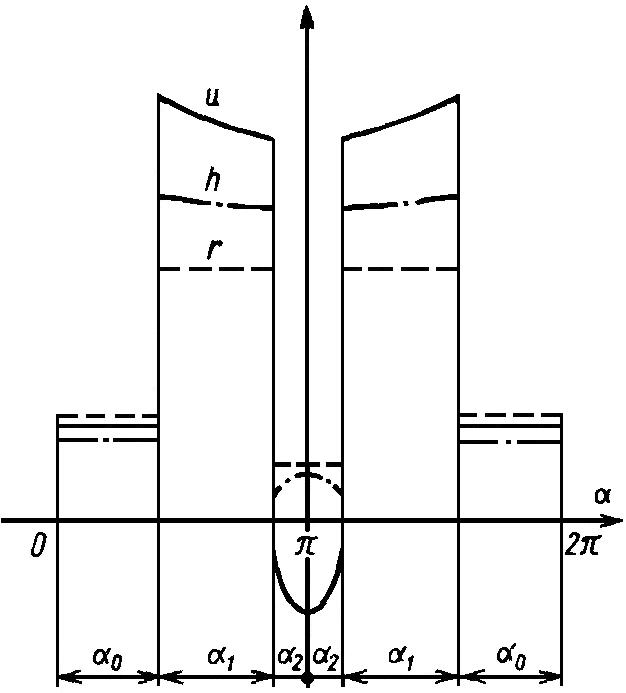
Главная составляющая гидродинамической скорости – это скорость скольжения, так как обычно r_a>2 r₂. На рис. 2.2 представлены диаграммы гидродинамической скорости, радиуса кривизны и относительной толщины изотермической пленки смазки без учета влияния нагрузки, которая, несмотря на большие изменения в кулачковых механизмах, мало влияет на толщину пленки.

На границах участка, определенного углом a₂, гидродинамическая скорость равна нулю, и ЭГД-пленка смазки может существовать только в результате явления выдавливания масла между взаимодействующими поверхностями, определяемого прямым ударом (может существовать также пленка граничной смазки). На рис. 2.2 можно также заметить, что на этой границе будет самая тонкая пленка, которая в действительности еще тоньше из-за большой доли скольжения. Одновременно это зона наибольшей нагрузки на контакт, в связи с чем необходимо особенно тщательно анализировать условия трения, тем более, что при угле a = a₂ гидродинамическая скорость равна разности скоростей скольжения и качения. В результате при неудачном подборе радиуса кулачка r₂> r_a/2 может полностью исчезнуть ЭГД-пленка смазочного материала. Для увеличения гидродинамической скорости в этой зоне надо уменьшить радиус кривизны кулачка r₂ до допустимого с точки зрения давления Герца минимума.

2.2 Методика расчета ЭГД-пленки смазки

      в кулачковых механизмах

Методику расчета ЭГД-пленки смазки в кулачковых механизмах рассмотрим на примере кулачкового механизма с тарельчатым толкателем со следующими исходными параметрами:

расстояние радиуса вершины кулачка от его центра –a = 30 мм;

радиус вершины кулачка – r₂ = 10 мм;

угол радиуса вершины кулачка – a ₂ = 5°;

ширина кулачка – b = 10 мм;

частота вращения кулачка – n = 2000 об/мин;

материал кулачка и толкателя – сталь;

модуль упругости для стали Е = 2,08∙10¹¹ Па;

кинематическая вязкость стали ν = 0,3 м²/с

нагрузка на кулачок на границе угла a ₂  – Р = 1500 Н;

рабочая температура – t = 50 °С;

смазочное масло – Hipol 15;

коэффициент вязкости при t – a = 0,015 МПа^-1;

динамическая вязкость при рабочей температуре η = 0,015 Нс/м²;

плотность масла ρ = 0,85 г/мм³;

коэффициент теплопроводности k = 0,15 Вт/(м×°С);

коэффициент зависимости вязкости от температуры β = 0,03.

Задание: Вычислить наименьшую толщину ЭГД-пленки смазки h _min.

Решение:

Приведенный ниже пример хорошо иллюстрирует возможность оценки режима ЭГД-смазки для различных неконформных узлов трения (кулачковых механизмов) на стадии проектирования и конструирования различных машин и механизмов.