Дифференциальные уравнения конвективного теплообмена

16.4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КОНВЕКТИВНОГО ТЕПЛООБМЕНА

В подразделе 8.5 дан вывод дифференциального уравнения теплопроводности в неподвижной среде, аналогичным образом можно вывести дифференциальное уравнение в движущейся среде, называемое уравнением энергии, которое в декартовых координатах имеет вид

или в более краткой записи:

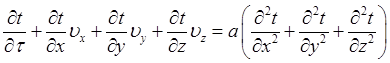               (10.3)

где ф — время,— проекции вектора скорости на оси х, у, z, м/с; а — температуропроводности, м²/с;

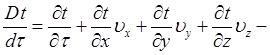
полная производная температура по времени ф, которую в связи с тем, что она связана с движущейся материей или субстанцией, называют субстанциальной производной и обозначают особым символом Dt/dx;

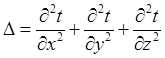^–оператор Лапласа.

Уравнение (10.3) описывает изменение температуры в точке х, у, z в неподвижной системе координат, при этом первый член левой части уравнения характеризует изменение температуры во времени, последующие члены левой части — изменение температуры вследствие движения жидкости через рассматриваемую точку пространства; правая часть уравнения выражает изменение температуры вследствие теплопроводности.

При уравнение энергии переходит в дифференциальное уравнение теплопроводности (8.12).

Для интегрирования уравнения (10.3) и расчета по нему температурного поля необходимо знать компоненты скорости Это приводит в общем случае к необходимости дополнительного рассмотрения уравнений движения {уравнений Навье — Стокса) и уравнения неразрывности потока. Уравнения движения для несжимаемой жидкости (с = const)
в проекциях на оси декартовых координат имеют вид:

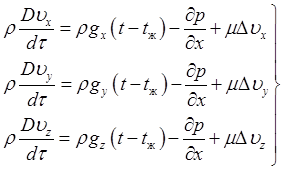                       (10.5)

                                                                                          119