Волновые процессы в атмосфере, страница 5

Обычно тангенс угла наклона поверхности раздела изменяется в пределах  0.005 – 0.02. В среднем полагают tga=0.01. Есть разница для случаев, когда теплая масса «наползает» на холодную, и когда холодная надвигается на теплую. Из-за трения о поверхность Земли в последнем случае у поверхности Земли образуется «тупой клин».    

Волновые движения на поверхности раздела

На поверхности раздела также могут возникать волновые движения. Это периодические колебания поверхности раздела наподобие волн на воде от брошенного камня (в последнем случае поверхность раздела – граница между воздухом и водой). Скорость распространения слабых возмущений на поверхности раздела может быть приближенно представлена в виде:   

                  .

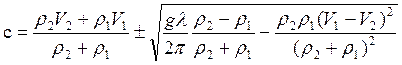Здесь l - длина волны. Первое слагаемое в этой формуле получило наименование конвективной скорости распространения волны.

Если V₁=V₂, r₂=r₁ (нет границы раздела), то с=V , то есть, конвективная скорость в этом случае просто совпадает со скоростью потока. Второе слагаемое – динамическая скорость существует только на действительной поверхности раздела.

Основное движение у поверхности раздела оказывается неустойчивым по отношению к малым возмущениям, если динамическая скорость становится мнимой. В этом случае возмущения с течением времени безгранично возрастают, и волновое движение невозможно.       В частности, движение неустойчиво, если r₂<r₁, то есть, холодный воздух расположен над теплым слоем.

Предельным случаем устойчивого волнового движения является длина волны l, при которой динамическая скорость обращается в нуль. Эта критическая длина волны тем больше, чем больше DV и чем меньше DT. При DT=4° и DV=20м/с  l_критич»9км. При DT=20° и DV= 20м/с  l_критич»2км.

Рассмотренный случай волновых движений иногда привлекают для объяснения природы волнистых облаков. Образование таких облаков тогда рассматривают как результат возникновения волн на поверхности раздела двух воздушных слоев, имеющих разную плотность и движущихся с различными скоростями. В области гребня волны имеет место восходящее движение воздуха, происходит конденсация пара и образование облаков. В области ложбин, где возникают нисходящие течения, воздух, наоборот, удаляется от насыщения. В результате образуются гряды волнистых облаков.

И еще несколько слов об устойчивости фронтальных поверхностей. Исследования показывают, что поверхность раздела тем более устойчива, чем больше относительная  скорость основных потоков по обе стороны раздела, и чем меньше высота разделенных воздушных масс, а также, чем меньше разрыв плотности воздуха.   

            Волны всех длин волн на поверхности раздела со сдвигом ветра неустойчивы. Если к этому добавляется разрыв плотности, неустойчивость проявляется только для длин волн, меньших критической:

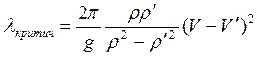 , где  и  плотности нижнего и верхнего слоев воздуха,  и  скорости ветра в них. Обычно критическая длина волны составляет около нескольких километров.

Рассмотренные волновые движения иллюстрируют физический подход к анализу периодических движений атмосферы, когда мы изначально интересовались природой возвращающей силы, приводящей к колебательному движению. Однако возможен и другой подход к проблеме, который уместно назвать динамическим или математическим. Суть его кратко сводится к следующему. Считается, что в первом приближении атмосфера совершает чисто зональные движения, подчиняющиеся геострофическим соотношениям. Очевидно, в таком случае скорость потока на заданной широте не зависит от долготы. Тогда разность между реальным движением и зональным можно представить в виде суперпозиции «волновых движений» вдоль кругов широты, которые собственно и определяют особенности движения воздуха на разных долготах.

В рамках такого подхода совсем не обязательно интересоваться причиной, вызвавшей тот или иной волновой процесс, поскольку волновые движения возникают непосредственно как решения уравнений для поправок к чисто зональному движению. Описанный способ весьма популярен в последние годы, так как позволяет выделить регулярное крупномасштабное зональное течение уже на начальном этапе решения задачи и свести проблему решения уравнений движения для реальной атмосферы к нахождению значительно более слабых по интенсивности поправок в виде набора волновых движений. К тому же существует возможность отказаться от упрощающей линеаризации уравнений для получающихся поправок и таким образом сохранить в рассмотрении нелинейные члены, анализ роли которых в последнее время привлекает внимание многих исследователей.