Механика: Учебно-методическое пособие для самостоятельного изучения и по решению задач

Апанасевич Е.Е., Бокатая Е.Л., Федоренчик Е.В.

«Пособие по решению задач по физике (Механика)»

Предисловие

Предлагаемое учебно-методическое пособие содержит краткое изложение основных положений по теоретической части курса «Механика», основные понятия, законы и формулы, знание которых необходимо для понимания и решения задач; примеры решения задач, охватывающие основные темы данного раздела; задачи для самостоятельного решения; а также варианты контрольной работы по курсу «Механика» для студентов заочного формы обучения. Структура и содержание учебно-методического пособия соответствуют программе курса «Механика».

Пособие предназначено для самостоятельного изучения курса «Механика» студентами 1-ого курса.

§1. Кинематика материальной точки

1.1 Кинематика поступательного движения материальной точки

Положение материальной точки в пространстве задается радиус-вектором , проведенным из начала координат выбранной системы отсчета в точку пространства, где в данный момент времени находится материальная точка. Закон движения материальной точки задается как функция времени в виде векторного уравнения

,                                                      (1.1)

где  − единичные векторы (орты), совпадающие с положительными направлениями соответствующих осей;  − координаты материальной точки и одновременно проекции радиус-вектора на координатные оси .

Кинематические уравнения движения в координатной форме:

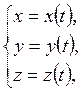                                                                     (1.2)

где  — время.

Модуль радиус вектора  определяется выражением

.                                               (1.3)

Вектор перемещения  материальной точки из точки с координатами  в точку :

.                            (1.4)

Модуль вектора перемещения

.                                      (1.5)

Средняя скорость перемещения − векторная величина, равная отношению вектора перемещения  материальной точки к промежутку времени , за который это перемещение произошло:

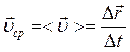.                                                                      (1.6)

Средняя путевая скорость − скалярная величина, равная отношению пройденного материальной точкой пути  к времени движения :

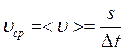.                                                            (1.7)

Мгновенная скорость − векторная величина, равная первой производной радиус-вектора материальной точки (тела) по времени:

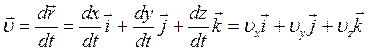,                                  (1.8)

где 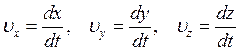 — проекции вектора скорости  на координатные оси , соответственно. Вектор скорости  направлен по касательной к траектории в данной точке.

Модуль скорости        .                                                        (1.9)

Среднее ускорение − векторная величина, равная отношению изменения скорости  материальной точки к промежутку времени , за который это изменение произошло

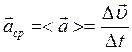.                                                                      (1.10)

Мгновенное ускорение − векторная величина, равная первой производной скорости материальной точки (тела) по времени:

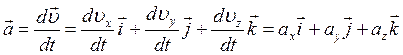,                            (1.11)

где 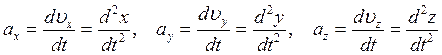 — проекции ускорения  на координатные оси , соответственно.

Модуль вектора ускорения

.                                                (1.12)

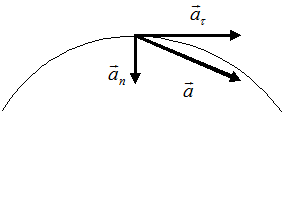
В случае криволинейного движения вектор ускорения  можно представить как сумму нормальной  и тангенциальной  составляющих (рис.1.1):

.                               (1.13)

Нормальное ускорение:

                                    (1.14)

составляющая ускорения, характеризующая изменение вектора скорости  материальной точки (тела) по направлению;  направлено по нормали  к траектории в данной точке (по радиусу кривизны  траектории).

Тангенциальное ускорение: 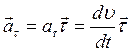                                                            (1.15)

составляющая ускорения, характеризующая изменение скорости  материальной точки (тела) по величине;  направлено по касательной к траектории в данной точке.

Модули этих ускорений:

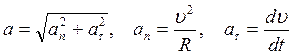                                       (1.16)

где  — радиус кривизны в данной точке траектории.

Основные формулы кинематики поступательного движения:

Ускорение  является первой производной скорости  материальной точки (тела) по времени:

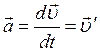;                                                             (1.17)

скорость материальной точки можно представить как первообразную от ускорения по времени:

;                                                       (1.18)

где  − скорость материальной точки в начальный момент времени .

Скорость  равна первой производной радиус-вектора  материальной точки (тела) по времени:

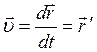;                                                              (1.19)

радиус-вектор  − первообразная вектора скорости по времени:

;                                                        (1.20)

где  − радиус-вектор материальной точки в начальный момент времени