Определение моментов инерции твердых тел с помощью трифилярного подвеса

Лабораторная работа

Определение моментов инерции твердых тел с помощью трифилярного подвеса

Принадлежности: трифилярный подвес; секундомер; линейка; штангенциркуль; набор тел, подлежащих измерению.

Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси имеет вид

,

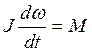где М – сумма проекций на ось всех моментов сил, действующих на тело, J – момент инерции тела, ω – его угловая скорость.

Это уравнение напоминает уравнение Ньютона для движения материальной точки: роль силы играет ее момент, роль скорости – угловая скорость, роль массы – момент инерции.

Момент инерции характеризует инерционные свойства твердого тела при вращательном движении. Чем больше момент инерции, тем труднее изменить скорость вращения тела.

Момент инерции материальной точки

,

где m – масса точки, r – расстояние до оси вращения.

Если тело состоит из нескольких материальных точек, то его момент инерции равен сумме моментов инерции каждой из точек.

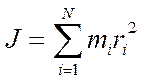
Момент инерции J сплошного тела относительно некоторой оси определяется выражением

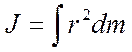
где r – расстояние элемента массы dm от оси вращения.

В простых случаях величину момента инерции можно определять расчетом.

Например:

момент инерции полого цилиндра (а также тонкого кольца, как частный случай полого цилиндра с малой высотой) относительно продольной оси J=mR² , где m – масса кольца, R – его радиус.

момент инерции однородного цилиндра (а также диска) относительно продольной оси J=(1/2)mR² , где m – масса цилиндра, R – его радиус;

момент инерции однородной сферы относительно оси, проходящей через центр масс, J=(2/5)mR² , где m – масса сферы, R – ее радиус;

момент инерции однородного стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, J=(1/12)mL² , где m – масса стержня, L – его длина;

момент инерции однородного прямоугольника относительно оси, проходящей через центр масс и перпендикулярной плоскости прямоугольника, J=(1/12)m(a²+b²), где m – масса прямоугольника, a и b – его длина и ширина;

Из вышеприведенных расчетов видно, что момент инерции тел зависит не только от массы тела, но также и от его формы. Например, момент инерции полого цилиндра отличается от момента инерции однородного цилиндра. В полом цилиндре каждая точка вносит одинаковый вклад в момент инерции, поскольку все точки находятся на одинаковом расстоянии от оси. В однородном цилиндре точки, расположенные ближе к оси, вносят меньший вклад в момент инерции. Поэтому при одинаковых массах момент инерции полого цилиндра больше момента инерции однородного цилиндра.

В тех случаях, когда распределение массы заранее неизвестно, момент инерции приходится находить экспериментальным путем. Одним из удобных методов измерения моментов инерции твердых тел является метод трифилярного подвеса.

Устройство такого подвеса показано на рис. 1. Подвижная платформа Р' подвешена к платформе Р на трех симметрично расположенных нитях AA’, ВВ’ и СС’. Платформа Р укреплена на вертикальной оси, вокруг которой она может вращаться с достаточно большим трением. Если платформу резко повернуть, то в системе возникнут крутильные колебания. Если повернуть нижнюю платформу Р’ вокруг вертикальной оси на некоторый угол φ₀ относительно верхней, то возникает момент