Исследование колебаний гибкой однородной струны, натянутой между двумя неподвижными точками

Лабораторная работа

Изучение колебаний струны

Цель работы: исследовать колебания гибкой однородной струны, натянутой между двумя неподвижными точками.

Принадлежности: рейка со струной, блок питания переменного напряжения, электромагнит, выпрямитель, динамометр, устройство натяжения, линейка.

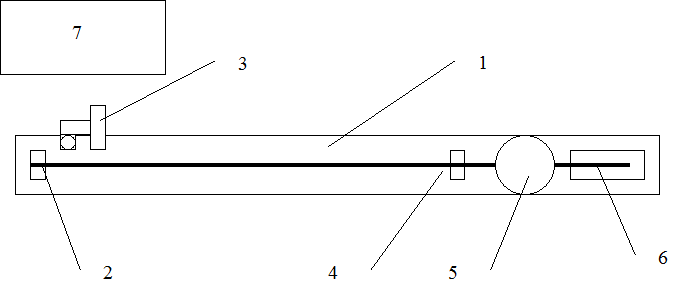
Рис. 1а. Схема установки для изучения колебаний струны.

На деревянной рейке 1 установлены упоры 2, 4 и электромагнит 3 с диодом и выключателем. Один конец струны закреплен на упоре 2, а другой пропущен через упор 4 и прикреплен к динамометру 5. С другой стороны динамометра к устройству натяжения протянут трос.

Рис.1б. Электрическая схема установки.

Когда выключатель замкнут, на электромагнит подается переменное напряжение частотой 50 Гц (см.рис.1б). При этом магнит притягивает струну 100 раз в секунду. Притяжение происходит как при положительной, так и при отрицательной полярности тока. Если выключатель разомкнут, то через магнит протекает ток только в течение половины периода. В течение другой половины периода ток отсутствует, поскольку ток через диод может протекать лишь в одну сторону.

Если в натянутой и закрепленной с обеих сторон струне возбудить колебания, то по струне побегут волны, которые отражаются от точек крепления и, складываясь друг с другом, создают сложную картину колебаний. Рассмотрим, как распространяются волны по струне. Для этого оттянем струну с одной стороны и затем отпустим. Созданное нами возмущение передвигается по струне, не меняя своей формы. Такое перемещающееся возмущение называется бегущей волной. В нашем случае отклонение частиц струны происходит в направлении, перпендикулярном направлению движения волны (направлению струны). Такие волны называются поперечными.

Скорость, с которой передвигается возмущение по струне, называется скоростью волны. Мы будем обозначать ее буквой v. Эта скорость не имеет ничего общего со скоростью u, которую приобретают частицы струны в процессе прохождения волны. Эти две скорости в поперечной волне перпендикулярны друг другу. Не равны и их численные значения. Скорость u зависит от того, насколько сильно была оттянута струна перед тем, как ее отпустили. Эта скорость непрерывно меняется во времени и меняет знак, когда частицы струны изменяют направление своего движения. Скорость волны v определяется только плотностью струны и ее натяжением.

Рассмотрим два положения волны: начальное и последующее.

Обозначим через Dt время смещения волны, а через Dx - расстояние между аналогичными точками на обеих кривых (поскольку форма возмущения при передвижении струны не меняется, величина Dx не зависит от выбора этих точек). Ясно, что

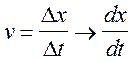.                                                           (1)

Как уже отмечалось, картина колебаний в струне создается наложенными друг на друга бегущими в разные стороны многократно отраженными волнами и, вообще говоря, нерегулярна и сложна. Можно, однако, заметить, что при определенном натяжении струны картина стабилизируется - в струне возбуждаются стоячие волны. Они нас и будут интересовать.

Гармонически зависящие от времени бегущие волны описываются уравнениями типа

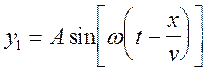                                                          (2)

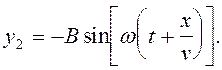                                                       (3)

В этих формулах y₁ и y₂ - смещения точек струны из положения равновесия, A и B - амплитуды, w - круговая частота волны, v - скорость перемещения волны. (Знак минус в формуле (3) не обязателен. Преимущество, возникающее от его введения, выяснится позднее.) Легко видеть, что волна (2) передвигается в сторону увеличения, а волна (3) - в сторону уменьшения x.

Рассмотрим результирующее волновое движение, составленное из волн (2) и (3):

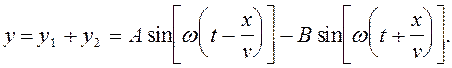
Перепишем y в виде

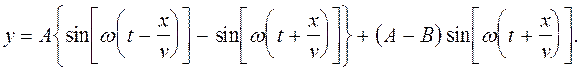               (4)

Преобразуем выражение, стоящее в фигурных скобках, по формуле для разности синусов двух углов ():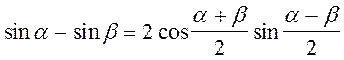

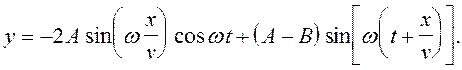                         (5)

При A= B в выражении (5) остается только первый член, описывающий