Высшая математика (комплексные числа, производные, интегралы, дифференциальные уравнения): Учебно-методическое пособие

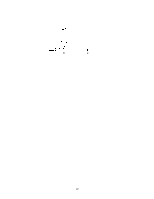
потом отмечаются точки экстремума, точки перегиба, точки пересечения с осями. Если этих точек недостаточно, то можно найти ещё несколько дополнительных точек.

            График данной функции изображен на рисунке.  

Неопределенный интеграл

Функция   называется первообразной для функции  , если  . Совокупность всех первообразных для функции  называется неопределенным интегралом от функции  и обозначается  , при этом   называется подынтегральной функцией,  – подынтегральным выражением.

Можно доказать, что ,  где   – некоторая первообразная для ,  – произвольная постоянная.

Для вычисления неопределенных интегралов нужно знать основные свойства, табличные интегралы и методы интегрирования.

Основные свойства неопределенных интегралов:

1. .

2. ,   где   – постоянная, не равная нулю.

3. .

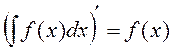4. .

Свойства 3 и 4 показывают, что операции дифференцирования и интегрирования являются взаимообратными.

Таблица неопределенных интегралов

1) 

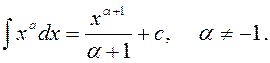
2) 

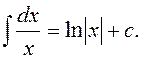
3) 

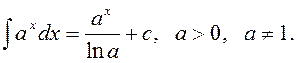
Если  ,  то  .

4) 

5) 

6) 

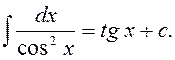
7) 

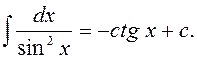
8) 

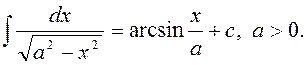
9) 

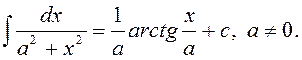
10) 

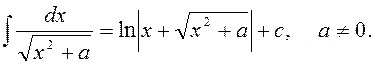
11) 

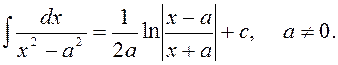
Все формулы справедливы также в случае, если переменную   заменить на некоторую другую функцию. Так, если в формуле 2 заменить x  на (sin x) , то получим, что

.

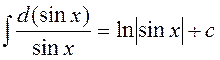Перейдем к рассмотрению методов интегрирования.

Непосредственное интегрирование

Преобразование подынтегрального выражения в целях получения табличного интеграла называется непосредственным интегрированием, при этом используется следующая формула:

.

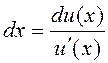Рассмотрим несколько примеров.

1. 

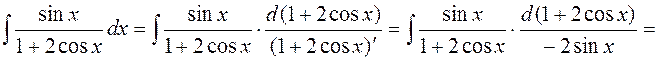
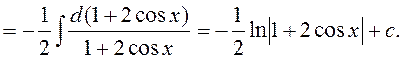
2)  .

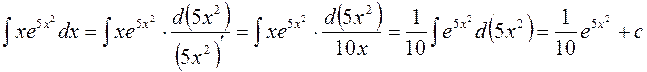3) 

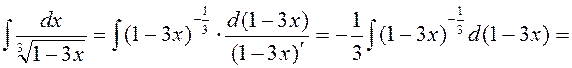
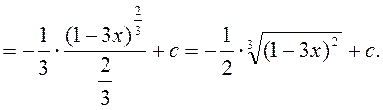
4) 

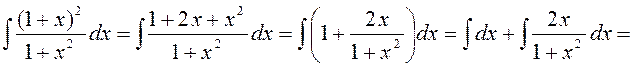
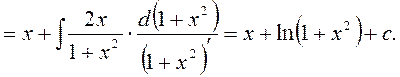
Интегрирование по частям

Формула интегрирования по частям имеет вид

,

поскольку  , то эту же формулу можно записать так:

.

Для того чтобы применить формулу интегрирования по частям, нужно подынтегральную функцию разбить на два множителя, один из них обозначить  , другой − . После этого найти   и  . Для нахождения функции   по заданной производной   можно вычислить неопределенный интеграл    и затем положить  .

При выборе функций   и  следует помнить, что функция  не должна быть сложной, иначе для нее будет трудно найти первообразную. В качестве   обычно выбирают функцию, которая упрощается при дифференцировании, например, логарифмическую или обратную тригонометрическую функцию. В частном случае за   можно взять подынтегральную функцию, тогда  и .

Пример. Вычислить  .

Решение. Положим  .  Тогда  .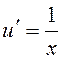

Найдем  ;   .

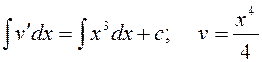Применим формулу интегрирования по частям:

.

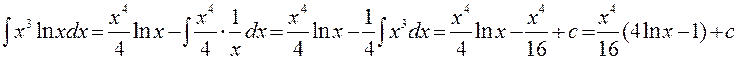Интегрирование подстановкой

В неопределенном интеграле   можно сделать подстановку (замену переменной)  , чтобы получить более простой интеграл.

.

Если подынтегральная функция является иррациональной, то нужно сделать такую подстановку, чтобы новая подынтегральная функция не содержала иррациональностей.

Пример. 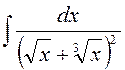   – интеграл от иррациональной функции.

Сделаем подстановку  , тогда    .

Таким образом,

.

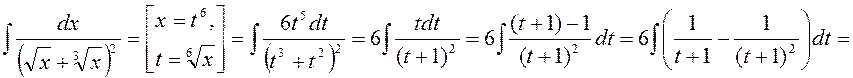
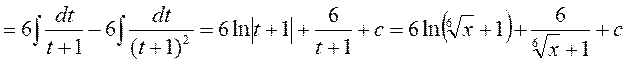Если подынтегральная функция зависит только от функций   и , то можно сделать универсальную тригонометрическую подстановку 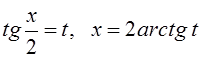 . В результате подынтегральная функция не будет содержать функций  и , так как

,

,

.

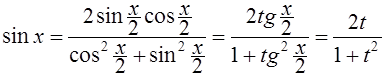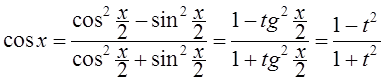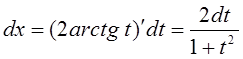Пример.

.

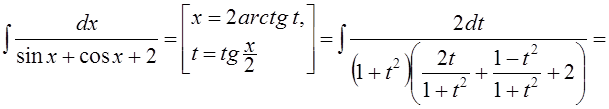
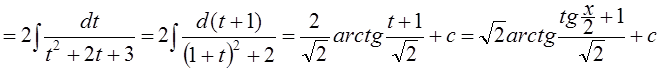Если подынтегральная функция зависит только от , то следует сделать подстановку  .

Данные интегралы можно вычислить, не используя универсальную тригонометрическую подстановку. Рассмотрим два примера.

1. 

.

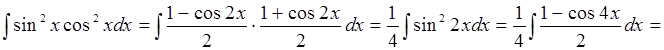
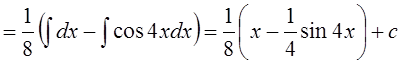2. 

.

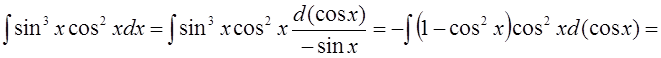
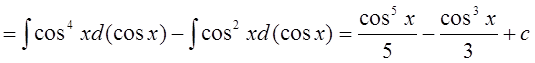Интегрирование рациональных функций

Отношение двух многочленов называется рациональной функцией. Если степень многочлена   в числителе меньше степени многочлена в знаменателе, то рациональная функция называется правильной, в противном случае – неправильной. Простейшими рациональными функциями называются функции вида

,

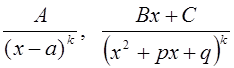где   – действительные числа;   – натуральное число и  .

Алгоритм интегрирования рациональной функции:

1. Если рациональная функция неправильная, то с помощью деления ее нужно представить в виде суммы многочлена и правильной рациональной функции.

2. Знаменатель правильной рациональной функции нужно разложить на линейные и квадратичные множители.

3. Используя метод неопределенных коэффициентов, разложить правильную рациональную функцию на сумму простейших.

4. Проинтегрировать все полученные слагаемые.

Пример.  Вычислить    .

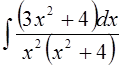Подынтегральная функция правильная, и ее знаменатель разложен на множители, поэтому переходим к третьему пункту алгоритма. Разложение на сумму простейших для этой функции будет иметь вид

,

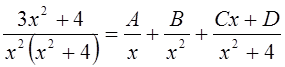где   – некоторые числа (неопределенные коэффициенты), которые нужно найти. Дроби в правой части приводим к общему знаменателю (он равен