Курс лекций по дифференциальным уравнениям для студентов-заочников.
Лекция 1. Общие понятия.
При изучении физических явлений часто возникают уравнения, связывающие неизвестную функцию и ее производные. Такие уравнения называются дифференциальными.
Примеры.
1. 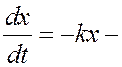 уравнение
радиоактивного распада(k−постоянная распада, x−количество
неразложившегося вещества в момент времени t, скорость
распада
уравнение
радиоактивного распада(k−постоянная распада, x−количество
неразложившегося вещества в момент времени t, скорость
распада ![]() пропорциональна количеству
неразложившегося вещества).
пропорциональна количеству
неразложившегося вещества).
2. 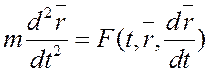 −
уравнение движения точки массой
−
уравнение движения точки массой ![]() под влиянием силы
под влиянием силы ![]() , зависящей от времени, положения точки,
определяемого радиус-вектором
, зависящей от времени, положения точки,
определяемого радиус-вектором ![]() , и ее скорости
, и ее скорости ![]() . Сила равна произведению массы на
ускорение.
. Сила равна произведению массы на
ускорение.
3. 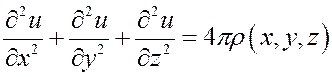 −уравнение
Пуассона, которому, например, удовлетворяет потенциал
−уравнение
Пуассона, которому, например, удовлетворяет потенциал ![]() электростатического
поля,
электростатического
поля, ![]() −плотность зарядов.
−плотность зарядов.
Нахождение неизвестных функций, определяемых дифференциальным уравнением, является основной задачей теории дифференциальных уравнений.
Если в дифференциальном уравнении неизвестные функции или вектор-функции являются функциями одной переменной, то дифференциальное уравнение называется обыкновенным(например, уравнения 1, 2). Если же неизвестная функция зависит от двух и более переменных, то уравнение называется уравнением в частных производных (например, уравнение 3).
Порядком дифференциального уравнения называется максимальный порядок входящей в уравнение производной неизвестной функции.
Решением дифференциального уравнения называется функция, которая при подстановке в дифференциальное уравнение, обращает его в тождество.
Например, уравнение радиоактивного распада
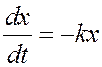
имеет решение
![]()
где c − произвольная постоянная.
Уравнение не вполне определяет закон распада ![]() . Нужно еще знать количество вещества
. Нужно еще знать количество вещества ![]() в момент времени
в момент времени ![]() .
Тогда, закон распада примет вид
.
Тогда, закон распада примет вид ![]() . Задача нахождения
. Задача нахождения ![]() при заданном начальном условии
при заданном начальном условии ![]() , называется задачей Коши.
, называется задачей Коши.
Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Не всегда решение находится в явном виде, как в рассмотренном примере. Однако, используя компьютеры, можно решить дифференциальное уравнение приближенно с большой точностью.
При интегрировании дифференциального уравнения обычно ставят цель найти все его решения. Например, в уравнении все решения получаются из решения при некотором выборе постоянной C. Решение называется общим решением уравнения . Решения дифференциального уравнения, получаемые из общего решения, называются частными. Однако, иногда не удается включить в общее решение все решения уравнения. Решения, не являющиеся частными, называются особыми.
Не всегда удается найти
решение в явном виде. Иногда оно задается неявно соотношением ![]() , называемым интегралом уравнения.
Соответственно, при неявном задании общего решения уравнения получается общий
интеграл уравнения
, называемым интегралом уравнения.
Соответственно, при неявном задании общего решения уравнения получается общий
интеграл уравнения ![]() .
.
Рассмотрим уравнение первого порядка
![]() ,
,
разрешенное относительно производной.
Пусть функция ![]() имеет своей областью определения некоторую
область
имеет своей областью определения некоторую
область ![]() , которая также является областью
определения уравнения . Обычно далее предполагается, что
, которая также является областью
определения уравнения . Обычно далее предполагается, что ![]() непрерывна в
непрерывна в ![]() .
Функция
.
Функция ![]() , непрерывная и непрерывно дифференцируемая
на
, непрерывная и непрерывно дифференцируемая
на ![]() , такая, что
, такая, что ![]() при
при ![]() ,
, ![]() ,
называется решением уравнения на
,
называется решением уравнения на ![]() .
.
Пример 4. Уравнение ![]() имеет решение
имеет решение ![]() .
Решением также будет являться любая функция вида
.
Решением также будет являться любая функция вида ![]() , где
, где ![]() − произвольная постоянная.
− произвольная постоянная.
Геометрически решению
уравнения соответствует линия, лежащая в области D
плоскости ![]() и представляющая собой график функции
и представляющая собой график функции ![]() . Эта линия называется интегральной
линией уравнения . Так как функция
. Эта линия называется интегральной
линией уравнения . Так как функция ![]() имеет
непрерывную производную
имеет
непрерывную производную ![]() , интегральная линия
имеет в каждой точке
, интегральная линия
имеет в каждой точке ![]() касательную, угловой коэффициент
которой определяется из уравнения
касательную, угловой коэффициент
которой определяется из уравнения ![]() .
.
Заметим, что общему решению
соответствует семейство кривых, а решению задачи Коши − интегральная кривая,
проходящая через точку ![]() .
.
Лекция 2.
Дифференциальные уравнения первого порядка.
2.1. Уравнения первого порядка, разрешенные относительно производной
Обыкновенные дифференциальные
уравнения первого порядка можно, разрешив относительно производной, представить
в виде . Простейший пример такого уравнения 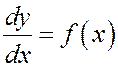 . В этом случае
. В этом случае ![]() содержит
произвольную постоянную, которая может быть определена, если известно значение
содержит
произвольную постоянную, которая может быть определена, если известно значение ![]() , тогда
, тогда 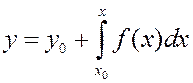 .
.
Вообще, при некоторых
ограничениях на функцию ![]() , уравнение
, уравнение 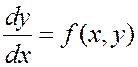 также имеет единственное решение,
удовлетворяющее условию
также имеет единственное решение,
удовлетворяющее условию ![]() , а его общее решение
зависит от одной произвольной постоянной.
, а его общее решение
зависит от одной произвольной постоянной.
2.2. Уравнения с разделяющимися переменными.
Дифференциальное уравнение вида
![]()
называется уравнением с
разделяющимися переменными. Функции ![]() и
и ![]() будем считать непрерывными. Если
будем считать непрерывными. Если ![]() − решение, то после подстановки его в и интегрирования, получим
− решение, то после подстановки его в и интегрирования, получим
![]() ,
,
где ![]() −
произвольная постоянная.
−
произвольная постоянная.
Мы получили уравнение , которому удовлетворяют все решения уравнения . И обратно, если ![]() удовлетворяет
, то после дифференцирования получим, что он
удовлетворяет и .
удовлетворяет
, то после дифференцирования получим, что он
удовлетворяет и .
Вполне возможно, что в
некоторых задачах ![]() и
и ![]() нельзя будет выразить в элементарных
функциях, однако в этом случае мы будем считать задачу интегрирования
дифференциального уравнения выполненной, поскольку мы свели ее к нахождению
неопределенных интегралов или квадратур.
нельзя будет выразить в элементарных
функциях, однако в этом случае мы будем считать задачу интегрирования
дифференциального уравнения выполненной, поскольку мы свели ее к нахождению
неопределенных интегралов или квадратур.
Если надо выделить частное
решение, удовлетворяющее условию ![]() , то оно, очевидно,
определится из уравнения
, то оно, очевидно,
определится из уравнения 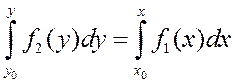 ,
которое получим из
,
которое получим из 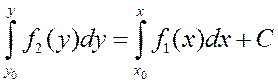 ,
воспользовавшись начальным условием
,
воспользовавшись начальным условием ![]() .
.
Пример 1. ![]() .
.
Переменные разделены,
поскольку при ![]() стоит функция
стоит функция
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.